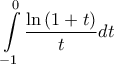Μεταφέρονται κάποια θέματα από το ποστ "Όρια με ολοκληρώματα" τα οποία εσφαλμένα τοποθέτησα εκεί αφού δεν υπεισέρχονται σε αυτά όρια.
Μεταφέρονται επίσης κάποια θεματάκια που αφορούσαν υπολογισμό και είχαν τοποθετηθεί στα ξεχωριστά ποστς.
"Γενικευμένο ολοκλήρωμα με λογαριθμικά 1", "Γενικευμένο ολοκλήρωμα με λογαριθμικά 2" και "Γενικευμένο ολοκλήρωμα με τριγωνομετρικά".
Ο κατάλογος θα συμπληρώνεται.
*****************************************************************************************
 Ας υπολογισθεί το
Ας υπολογισθεί το  .
.

 . Τότε
. Τότε 



 Έστω
Έστω  και
και  .
.  .
.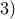 Έστω
Έστω  . Ας υπολογισθεί το
. Ας υπολογισθεί το 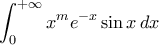 .
. Έστω
Έστω  . Ας υπολογισθεί το ολοκλήρωμα
. Ας υπολογισθεί το ολοκλήρωμα .
.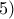 Έστω
Έστω 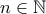 . Για
. Για 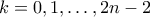 , ορίζουμε
, ορίζουμε 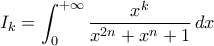 .
. 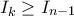 για
για  Υπολογισθήτω το ολοκληρωματάκι
Υπολογισθήτω το ολοκληρωματάκι  .
.



 .
.
![\displaystyle{I'\left( a \right) = - \int\limits_0^{ + \infty } {\frac{{{e^{ax}}}}{{{{({e^{ax}} + 1)}^2}}}} \,dx = \left[ {\frac{1}{{a\left( {1 + {e^{ax}}} \right)}}} \right]_0^{ + \infty } = -\frac{1}{{2a}}} \displaystyle{I'\left( a \right) = - \int\limits_0^{ + \infty } {\frac{{{e^{ax}}}}{{{{({e^{ax}} + 1)}^2}}}} \,dx = \left[ {\frac{1}{{a\left( {1 + {e^{ax}}} \right)}}} \right]_0^{ + \infty } = -\frac{1}{{2a}}}](/forum/ext/geomar/texintegr/latexrender/pictures/ad76c528c0ccfbe37e0e8bd2db04d245.png)




![\displaystyle{ = \int\limits_0^{ + \infty } {\left[ {\frac{1}{{x({e^{bx}} + 1)}} - \frac{1}{{x({e^{ax}} + 1)}}} \right]} \,dx} \displaystyle{ = \int\limits_0^{ + \infty } {\left[ {\frac{1}{{x({e^{bx}} + 1)}} - \frac{1}{{x({e^{ax}} + 1)}}} \right]} \,dx}](/forum/ext/geomar/texintegr/latexrender/pictures/ddbacabf76970735920458cd65ee26d0.png)

![\displaystyle{I\left( b \right) = \int\limits_0^{ + \infty } {\left[ {\frac{1}{{x({e^{bx}} + 1)}} - \frac{1}{{x({e^{bx}} + 1)}}} \right]} \,dx = 0 \Rightarrow \frac{{\ln b}}{2} + c = 0 \Rightarrow c = - \frac{{\ln b}}{2}} \displaystyle{I\left( b \right) = \int\limits_0^{ + \infty } {\left[ {\frac{1}{{x({e^{bx}} + 1)}} - \frac{1}{{x({e^{bx}} + 1)}}} \right]} \,dx = 0 \Rightarrow \frac{{\ln b}}{2} + c = 0 \Rightarrow c = - \frac{{\ln b}}{2}}](/forum/ext/geomar/texintegr/latexrender/pictures/94ba5f6927c75cb2338bef557fd39f57.png)

 συμπεριφέρεται κοντά στο 0 όπως η
συμπεριφέρεται κοντά στο 0 όπως η  η οποία δεν είναι ολοκληρώσιμη.
η οποία δεν είναι ολοκληρώσιμη. έχουμε ότι
έχουμε ότι πολύ μικρό μπορούμε να βρούμε
πολύ μικρό μπορούμε να βρούμε  με
με  άρα
άρα  .
.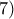 Ας υπολογισθεί το ολοκλήρωμα :
Ας υπολογισθεί το ολοκλήρωμα : 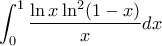
 Ας υπολογισθεί το ολοκλήρωμα
Ας υπολογισθεί το ολοκλήρωμα  όπου
όπου  .
.


 .
.