The task is to numerically estimate an integral. Here is the setting: suppose
 is a bounded real-valued function,
is a bounded real-valued function,  , defined on the unit interval
, defined on the unit interval  . You are not told anything more about the function
. You are not told anything more about the function  explicitly but you have access to a friendly oracle: if you prompt her with any given value
explicitly but you have access to a friendly oracle: if you prompt her with any given value 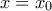 , she will loop up the function value
, she will loop up the function value  and whisper it to you. Your task is to estimate the value
and whisper it to you. Your task is to estimate the value  . \newline
. \newlineSelect
 independently at random from the uniform distribution on the unit interval, obtain the values
independently at random from the uniform distribution on the unit interval, obtain the values  from your friendly oracle, and boldly evaluate and proffer the value
from your friendly oracle, and boldly evaluate and proffer the value ![\hat{J_n} := \frac{1}{n} [\psi(X_1) + ...+\psi(X_n)] \hat{J_n} := \frac{1}{n} [\psi(X_1) + ...+\psi(X_n)]](/forum/ext/geomar/texintegr/latexrender/pictures/d1da40bc6e9491a1b215b358f70dfb4a.png) as your estimate of
as your estimate of  . A common, garden variety laptop can compute your estimate
. A common, garden variety laptop can compute your estimate  in a fraction of a second if
in a fraction of a second if  but is it any good? In defence of your starting procedure, with
but is it any good? In defence of your starting procedure, with  , estimate
, estimate  , the probability that your estimate makes an error of more than one percent. [Hint: if
, the probability that your estimate makes an error of more than one percent. [Hint: if  Uniform[0,1], stare at the expression for
Uniform[0,1], stare at the expression for  ]
]
 , όπου
, όπου  είναι μια φραγμένη πραγματική συνάρτηση, και
είναι μια φραγμένη πραγματική συνάρτηση, και  ορισμένη στο διάστημα μονάδας
ορισμένη στο διάστημα μονάδας  .
. . Θα επιλέξουμε τυχαία
. Θα επιλέξουμε τυχαία  από μια ομοιόμορφη κατανομή στο διάστημα μονάδας και θα λάβουμε τις τιμές
από μια ομοιόμορφη κατανομή στο διάστημα μονάδας και θα λάβουμε τις τιμές 
 ως:
ως:
 είναι το ολοκλήρωμα της
είναι το ολοκλήρωμα της 
 μπορεί να υπολογιστεί ως:
μπορεί να υπολογιστεί ως:
 , που σημαίνει
, που σημαίνει  . Έτσι:
. Έτσι:
 είναι η τετραγωνική ρίζα της διακύμανσης:
είναι η τετραγωνική ρίζα της διακύμανσης:  .
.

 , μπορούμε να υπολογίσουμε την πιθανότητα σφάλματος.
, μπορούμε να υπολογίσουμε την πιθανότητα σφάλματος.