 κοντά στο
κοντά στο  .
.Μπορούμε να χρησιμοποιούμε το θεώρημα αν είναι
 κοντά στο
κοντά στο  ; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;
; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;Συντονιστής: spyros
 κοντά στο
κοντά στο  .
. κοντά στο
κοντά στο  ; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;
; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;Γιώργος Απόκης έγραψε:Στο σχολικό αναφέρει ότι για να εφαρμόσουμε το Κριτήριο Παρεμβολής, πρέπει να ισχύεικοντά στο
.
Μπορούμε να χρησιμοποιούμε το θεώρημα αν είναικοντά στο
; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;
 είναι ίσα.
είναι ίσα. καλύπτει και την περίπτωση
καλύπτει και την περίπτωση  .
.Ναι, ξεκάθαρο είναι τώρα! Ευχαριστώ Μπάμπη!Μπάμπης Στεργίου έγραψε: Το γεγονός ότι η διάταξη στην περίπτωση που αναφέρεις είναι γνήσια , ουδόλως επηρεάζει την εφαρμογή του θεωρήματος, αφού η διάταξη του βιβλίου(με το ''='' καλύπτει και τη γνήσια.
Mπάμπης
Γιώργο, νομίζω ότι πρέπει να δώσεις να καταλάβουν οι μαθητές, καταρχήν τον ορισμό:Γιώργος Απόκης έγραψε:Στο σχολικό αναφέρει ότι για να εφαρμόσουμε το Κριτήριο Παρεμβολής, πρέπει να ισχύεικοντά στο
.
Μπορούμε να χρησιμοποιούμε το θεώρημα αν είναικοντά στο
; Πώς θα δικαιολογήσει ο μαθητής το αποτέλεσμα;
 .
. ( γιατί
( γιατί 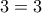 ) και
) και  ( γιατί
( γιατί  ).
). . Το αντίστροφο δεν αληθεύει. Για παράδειγμα ισχύει
. Το αντίστροφο δεν αληθεύει. Για παράδειγμα ισχύει  , αλλά δεν ισχύει
, αλλά δεν ισχύει  .
. , κοντά στο
, κοντά στο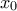
 , κοντά στο
, κοντά στο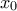 .
. είναι:
είναι:
 .
. είναι
είναι 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες