Αγαπητοί φίλοι,
όπως και αλλού έγραψα, αρκετό καιρό έχουμε να τα πούμε Γεωμετρικά και ομολογώ ότι μου λείψατε.
Ο λόγος της απουσίας μου είναι άσχετος με τη θέλησή μου και οφείλεται στις θερινές διακοπές, αλλά και κυρίως στο ότι ήμουν και είμαι απορροφημένος στη μελέτη διαφόρων Γεωμετρικών θεμάτων, από την οποία είχα νέα και πλούσια Γεωμετρική «συγκομιδή», της οποίας μερικά στοιχεία (όσα μπορέσω), θα δώσω εδώ.
Η Γεωμετρική αυτή «συγκομιδή», είναι Χαλκιδικιώτικη, Παριώτικη και Καλαμαριώτικη, ανάλογα με τον τόπο που βρέθηκα.
Τα παραπάνω αναφερόμενα πολύ φρέσκα και πρωτοεμφανιζόμενα πιστεύω στοιχεία Γεωμετρίας, αναφέρονται σε διάφορα Γεωμετρικά θέματα, όπως θεωρία:
-περί Επιπέδων Συμμετρικών Δεσμών των πέντε ακτινών,
-περί Συμμετρικών Σημειοσειρών των πέντε σημείων,
-περί Επιπέδων Συμμετροαρμονικών Δεσμών των πέντε ακτινών,
-περί Συμμετροαρμονικών Σημειοσειρών των πέντε σημείων,
-περί Επιπέδων Συμμετροδιαμεσικών Δεσμών των πέντε ακτινών,
-περί Συμμετροδιαμεσικών Σημειοσειρών των πέντε σημείων,
-περί Επιπέδων Συμμετροορθηκών Δεσμών των πέντε ακτινών,
-περί Συμμετροορθηκών Σημειοσειρών των πέντε σημείων,
-περί Ενέλίξης Σημειοσειρών,
-επέκταση Ενέλίξης και σε κύκλο, κτλ,
-περί Ημικανονικών Σχημάτων, κτλ,
-περί Ειδικών Εξαγώνων, κτλ.
Για τις θεωρίες των παραπάνω Γεωμετρικών θεμάτων, προέκυψαν και συνοδεύουν αυτές πολλές Γεωμετρικές Προτάσεις, Κατασκευές, ασκήσεις, εφαρμογές, κτλ, με τις αποδείξεις τους, που αναφέρονται σε ιδιότητες τούτων και που είναι διαφόρων βαθμών δυσκολίας.
Όλα τα παραπάνω αναφερόμενα έχουν έναυσμα κάποια από τις Προτάσεις που στο mathematica, συζητήθηκαν.
Μερικά (όσα μπορέσω), από τα παραπάνω αναφερόμενα έχω τη χαρά να προσπαθήσω εδώ να δώσω, για τους φίλους της Γεωμετρίας. Πιστεύω ότι έχουν πολλά να πάρουν αλλά και πολλά να δώσουν, συνεισφέροντας και τις δικές τους Προτάσεις- απόψεις και ακόμη κάνοντας και σχετική καλοπροαίρετη κριτική, ώστε να βελτιωθεί και η προσπάθεια αυτή.
Ξεκινάμε με την παρακάτω πρωτοεμφανιζόμενη πιστεύω Κατασκευή, την οποία και προτείνω για λύση, στους ενδιαφερομένους φίλους της Γεωμετρίας:
10ι(189). Δίνεται ευθεία
 και τα διατεταγμένα σημεία της
και τα διατεταγμένα σημεία της  , με
, με  .
.Στην ευθεία
 να ορισθεί σημείο
να ορισθεί σημείο  , για το οποίο να είναι:
, για το οποίο να είναι: . (1).
. (1).ή
 . (2).
. (2).Σχόλιο.
Την Κατασκευή αυτή έχω καταχωρίσει στην παράγραφο 10ι(189) του τόμου 10 του βιβλίου μου «Νέα Στοιχεία Γεωμετρίας» και έχω δώσει δύο λύσεις.
Καλή επιτυχία.
Με Γεωμετρική αγάπη,
Νίκος Κυριαζής.
*Το περιεχόμενο της εργασίας αυτής, με ανάγκασε στην αλλαγή αυτή. Όποιος μελετήσει σε βάθος την εργασία αυτή θα πεισθεί για την ανάγκη της αλλαγής.

 αντί
αντί  και
και  αντί
αντί  λόγω του σχεδιαστικού μου προγράμματος).
λόγω του σχεδιαστικού μου προγράμματος). και επ' αυτής λαμβάνουμε
και επ' αυτής λαμβάνουμε  . Από το
. Από το  της
της  . Φέρνουμε την
. Φέρνουμε την  μέχρι να τμήσει την
μέχρι να τμήσει την  στο
στο  .
.  με διατέμνουσα την
με διατέμνουσα την  έχουμε
έχουμε .
.  έχουμε
έχουμε 
 , το
, το  και των
και των  .
. μέχρι να τμήσει την
μέχρι να τμήσει την  και φέρνουμε την
και φέρνουμε την  μέχρι να τμήσει την
μέχρι να τμήσει την  στο
στο  . Εργαζόμαστε τώρα με θεώρημα Ceva στο
. Εργαζόμαστε τώρα με θεώρημα Ceva στο  . Τέλος παίρνουμε στο
. Τέλος παίρνουμε στο  το
το  .
. . To δεξί μέλος είναι δοθέν και κατασκευάζεται ως εξής: Κατασκευάζουμε τετράγωνα
. To δεξί μέλος είναι δοθέν και κατασκευάζεται ως εξής: Κατασκευάζουμε τετράγωνα  ισεμβαδικά με τα
ισεμβαδικά με τα  , αντίστοιχα. Η κατασκευή είναι στα Στοιχεία. Μετά κατασκευάζουμε τον λόγο
, αντίστοιχα. Η κατασκευή είναι στα Στοιχεία. Μετά κατασκευάζουμε τον λόγο  και τέλος χωρίζουμε το
και τέλος χωρίζουμε το  στο
στο  . Και αυτές οι κατασκευές είναι στα Στοιχεία. Τελιώσαμε.
. Και αυτές οι κατασκευές είναι στα Στοιχεία. Τελιώσαμε. μεταξύ των
μεταξύ των  τριγώνου
τριγώνου  , τέμνουν την πλευρά του
, τέμνουν την πλευρά του  και αν
και αν  είναι η διχοτόμος της γωνίας
είναι η διχοτόμος της γωνίας  =1, (1).
=1, (1). =1. (1’).
=1. (1’). και αν αληθεύει μία από τις δύο παραπάνω σχέσεις, τότε οι
και αν αληθεύει μία από τις δύο παραπάνω σχέσεις, τότε οι 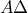 ,
,  είναι ισογώνιες.
είναι ισογώνιες. είναι ισογώνιες στο τριγώνο
είναι ισογώνιες στο τριγώνο  .
. . Αν το ζεύγος των σημείων
. Αν το ζεύγος των σημείων  τέμνει αρμονικά τα τμήματα
τέμνει αρμονικά τα τμήματα  και
και  , το ζεύγος των σημείων
, το ζεύγος των σημείων  τέμνει αρμονικά τα τμήματα
τέμνει αρμονικά τα τμήματα  και
και  , αν
, αν  είναι τα μέσα των τμημάτων
είναι τα μέσα των τμημάτων  αντίστοιχα και αν
αντίστοιχα και αν  , να βρεθεί ζεύγος σημείων
, να βρεθεί ζεύγος σημείων  , από τα οποία:
, από τα οποία: , να φαίνονται με ορθές γωνίες (Τα
, να φαίνονται με ορθές γωνίες (Τα  , να φαίνονται με γωνίες 45 μοιρών.
, να φαίνονται με γωνίες 45 μοιρών. , να φαίνονται με
, να φαίνονται με  ορθής γωνίας.
ορθής γωνίας. , είναι αρμονική.
, είναι αρμονική. με
με  . Να αποδειχθεί ότι υπάρχει σημείο
. Να αποδειχθεί ότι υπάρχει σημείο  .
. με
με  .
. και ένα μόνο ζεύγος σημείων
και ένα μόνο ζεύγος σημείων  .
.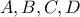 κείμενα σε άξονα με αρχή το
κείμενα σε άξονα με αρχή το  ) και
) και  . Με δεδομένα τα σημεία
. Με δεδομένα τα σημεία  και
και 
 το οποίο με δεδομένο ότι
το οποίο με δεδομένο ότι  έχει λύση το μοναδικό ζεύγος (η λύση δεν θα χρειαστεί, η μοναδικότητα μας ενδιαφέρει τελικά):
έχει λύση το μοναδικό ζεύγος (η λύση δεν θα χρειαστεί, η μοναδικότητα μας ενδιαφέρει τελικά):
 ,
, 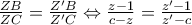
 πρέπει
πρέπει  και
και  , οπότε προκύπτει ως λύση το μοναδικό ζεύγος (και πάλι η λύση δεν θα χρειαστεί, η μοναδικότητα μας ενδιαφέρει):
, οπότε προκύπτει ως λύση το μοναδικό ζεύγος (και πάλι η λύση δεν θα χρειαστεί, η μοναδικότητα μας ενδιαφέρει):
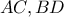 . Λόγω συμμετρίας ως προς τον άξονά μας, αναφερόμαστε, εν συνεχεία, μόνο στο
. Λόγω συμμετρίας ως προς τον άξονά μας, αναφερόμαστε, εν συνεχεία, μόνο στο  Πραγματικά, για αρχή είναι (εύκολο και γνωστό):
Πραγματικά, για αρχή είναι (εύκολο και γνωστό):
 του τριγώνου
του τριγώνου  τέμνουν τον άξονα σε σημεία τα οποία (εύκολο) διαιρούν τα
τέμνουν τον άξονα σε σημεία τα οποία (εύκολο) διαιρούν τα  αρμονικά, άρα αυτά είναι τα
αρμονικά, άρα αυτά είναι τα  όπως προκύπτει από την μοναδικότητα των
όπως προκύπτει από την μοναδικότητα των 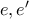 . Είναι
. Είναι
 του τριγώνου
του τριγώνου  , (που συμπίπτουν με αυτές της γωνίας
, (που συμπίπτουν με αυτές της γωνίας  του τριγώνου
του τριγώνου 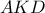 ), με τον άξονα. Ακόμα
), με τον άξονα. Ακόμα
 έίναι εσωτερική και εξωτερική διχοτόμος αντίστοιχα της γωνίας
έίναι εσωτερική και εξωτερική διχοτόμος αντίστοιχα της γωνίας  του τριγώνου
του τριγώνου  , άρα τα
, άρα τα  , με την πρόταση ότι ο περιγεγραμμένος κύκλος ενός τριγώνου τέμνει ορθογώνια κάθε Aπολλώνειο κύκλο του τριγώνου, προκύπτει απευθείας ότι το
, με την πρόταση ότι ο περιγεγραμμένος κύκλος ενός τριγώνου τέμνει ορθογώνια κάθε Aπολλώνειο κύκλο του τριγώνου, προκύπτει απευθείας ότι το  βλέπει τα
βλέπει τα  υπό ορθές γωνίες, και άμεσα πλέον οι
υπό ορθές γωνίες, και άμεσα πλέον οι  είναι εσωτερική και εξωτερική διχοτόμος αντίστοιχα της γωνίας
είναι εσωτερική και εξωτερική διχοτόμος αντίστοιχα της γωνίας  του τριγώνου
του τριγώνου  , και τα πάντα όλα προκύπτουν με απλή επαλήθευση.
, και τα πάντα όλα προκύπτουν με απλή επαλήθευση.