 , τριγώνου
, τριγώνου  , θεωρούμε σημεία
, θεωρούμε σημεία  αντίστοιχα , ώστε :
αντίστοιχα , ώστε :  .
.Η ευθεία η οποία διέρχεται από τα μέσα
 των
των 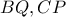 , τέμνει τις
, τέμνει τις  στα σημεία
στα σημεία  ,
, αντίστοιχα . Δείξτε ότι :
 και :
και : 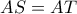 .
.Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , τριγώνου
, τριγώνου  , θεωρούμε σημεία
, θεωρούμε σημεία  αντίστοιχα , ώστε :
αντίστοιχα , ώστε :  .
. των
των 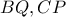 , τέμνει τις
, τέμνει τις  στα σημεία
στα σημεία  ,
,  και :
και : 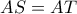 .
. , διατέμνουσας
, διατέμνουσας  έχω:
έχω: 
 διατέμνουσας
διατέμνουσας  έχω:
έχω: 
 και
και  παίρνω:
παίρνω:
Διαιρώντας κατά μέλη τις
 και
και  παίρνω:
παίρνω:
 φέρνω παράλληλες στην
φέρνω παράλληλες στην  και τέμνουν τις
και τέμνουν τις  στα
στα  .
. Ας είναι ακόμα ,
Ας είναι ακόμα ,  .
.

 έχω:
έχω:  και λόγω της
και λόγω της  :
:  και
και 
 είναι ισοσκελή τραπέζια και αναγκαστικά το τρίγωνο
είναι ισοσκελή τραπέζια και αναγκαστικά το τρίγωνο  ισοσκελές .
ισοσκελές . της ευθείας
της ευθείας  ώστε
ώστε  Προφανώς τα
Προφανώς τα  είναι
είναι 

 και
και 

Έστω
 το συμμετρικό του
το συμμετρικό του  ως προς το μέσο
ως προς το μέσο  της
της  και ας είναι
και ας είναι 
 παραλληλόγραμμο (οι διαγώνιες διχοτομούνται) και
παραλληλόγραμμο (οι διαγώνιες διχοτομούνται) και  (συνδέει τα μέσα των πλευρών τριγώνου)
(συνδέει τα μέσα των πλευρών τριγώνου)  προκύπτει ότι το τρίγωνο
προκύπτει ότι το τρίγωνο  είναι ισοσκελές άρα και τα
είναι ισοσκελές άρα και τα  είναι ισοσκελή (παράλληλες πλευρές) οπότε
είναι ισοσκελή (παράλληλες πλευρές) οπότε 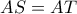 και με
και με  και το ζητούμενο έχει αποδειχθεί.
και το ζητούμενο έχει αποδειχθεί.O μέσον της
 . Είναι τότε
. Είναι τότε  (1) &
(1) &  (2) και επειδή
(2) και επειδή  έπεται ότι
έπεται ότι 
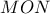 είναι ισοσκελές.
είναι ισοσκελές. συνεπώς επειδή
συνεπώς επειδή  έπεται ότι
έπεται ότι  άρα
άρα  παραλληλόγραμμο άρα
παραλληλόγραμμο άρα  .
.  συνεπώς τρίγωνο
συνεπώς τρίγωνο  ισοσκελές και
ισοσκελές και  οεδ
οεδ και τριγ
και τριγ  ισοσκελές έχουμε (γωνίες)
ισοσκελές έχουμε (γωνίες) άρα
άρα  ισοσκελές, συνεπώς
ισοσκελές, συνεπώς 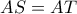
Για το δεύτερο ερώτημα
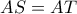 .
.
 είναι ισοσκελές και
είναι ισοσκελές και ακόμη
ακόμη 

Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 3 επισκέπτες