Αρχιμήδης Καλή επιτυχία.

Karanus · #41

Συμφωνώ απολύτως με την τοποθέτηση του κ. Στεργίου , όπως και με την παρατήρηση του κ.Λουρίδα , στο τέλος του κειμένου του για τους πραγματικά αξιόλογους μαθηματικούς που γράφουν στο

.

S.E.Louridas · #42

... Πάντως, δυσκολεύομαι να φανταστώ διδάσκοντα το Μάθημα της Γεωμετρίας, αλλά και συμβουλάτορα γιά το πώς να επιλύεται ένα Γεωμετρικό πρόβλημα, ακόμα και στις πρώτες τάξεις που αναφερόμαστε στους κύκλους που να μήν λέει:
Όταν έχεις τεμνόμενους κύκλους θεώρησε (φέρε) αμέσως τη κοινή τους χορδή και όταν έχεις εφαπτόμενους θεώρησε (φέρε) αμέσως την κοινή τους εφαπτομένη στο σημείο επαφής...

Και βέβαια για τον Ξεχασιάρη που δεν θεωρεί (φέρει) εκείνη τη στιγμή την κοινή εφαπτομένη των κύκλων στο σημείο

, κάποιος του «ψιθυρίζει στο αυτάκι» την εξής διαπραγμάτευση:

$\begin{array}{*{20}c} {\vartriangle AO_1 E \sim \vartriangle AOB\,\;\left( {\angle EAO_1 = \angle BAO} \right) \Rightarrow } \\ {\angle AO_1 E = \angle AOB \Rightarrow \angle Z = \angle C,\;\,\dot o\mu o\iota \alpha \;\,\angle B = \angle E} \\ \end{array}$

κ.τ.λ., κ.τ.λ.

S.E.Louridas

Κώστας Παππέλης · #43

Όχι Σιλουανέ δεν ξέχασες καμία περίπτωση... Ενδεχομένως να είπες και πιο πολλές (κατά την άποψή μου πάντα βέβαια)

Θερμά συγχαρητήρια και από εμένα!

#44

Μπορεί κάποιος να βάλει και τα υπόλοιπα θέματα;

#45

Συγχαρητήρια και από εμένα στους επιτυχόντες και ιδιαίτερα στα μέλη του

.

#46

Τα συγχαρητήρια στα παιδιά που διακρίθηκαν τα έχουμε ήδη δώσει και πραγματικά τα αξίζουν με το παραπάνω !

Θα ήθελα όμως να τα παρακαλέσω , όπως και όλους τους μαθητές που αγαπούν τα μαθηματικά , να αγκαλιάσουν με την ενεργή παρουσία τους το mathematica για πολλούς και ευνόητους λόγους.

Εδώ, εκτός από πλούσιο υλικό και χρήσιμες οδηγίες , κοντά σε έμπειρους δασκάλους και πρώην ολυμπιονίκες, θα βρουν ζεστασιά και δύναμη να συνεχίσουν ή να εντείνουν την προσπάθειά τους σε αυτόν τον όμορφο μεν αλλά σκληρό και συχνά μοναχικό δρόμο της κατάκτησης της μαθηματικής γνώσης.

Όσοι μαθητές είναι ήδη μέλη μας, ας παρακινούν ,σε κάθε ευκαιρία ,φίλους και γνωστούς τους να πλαισιώσουν δυναμικά το mathematica για να είναι όλοι συνοδοιπόροι σε μια χωρίς προηγούμενο μαθηματική εκστρατρεία, όπως είναι αυτή που βιώνουμε σε αυτή την ιστοσελίδα.Η εμπειρία που θα αποκομίσουν θα τους συνοδεύει σε όλη τους τη ζωή.

Μπάμπης

S.E.Louridas · #47

Μπάμπης Στεργίου έγραψε:Τα συγχαρητήρια στα παιδιά που διακρίθηκαν τα έχουμε ήδη δώσει και πραγματικά τα αξίζουν με το παραπάνω !

Θα ήθελα όμως να τα παρακαλέσω , όπως και όλους τους μαθητές που αγαπούν τα μαθηματικά , να αγκαλιάσουν με την ενεργή παρουσία τους το mathematica για πολλούς και ευνόητους λόγους.

Εδώ, εκτός από πλούσιο υλικό και χρήσιμες οδηγίες , κοντά σε έμπειρους δασκάλους και πρώην ολυμπιονίκες, θα βρουν ζεστασιά και δύναμη να συνεχίσουν ή να εντείνουν την προσπάθειά τους σε αυτόν τον όμορφο μεν αλλά σκληρό και συχνά μοναχικό δρόμο της κατάκτησης της μαθηματικής γνώσης.

Όσοι μαθητές είναι ήδη μέλη μας, ας παρακινούν ,σε κάθε ευκαιρία ,φίλους και γνωστούς τους να πλαισιώσουν δυναμικά το mathematica για να είναι όλοι συνοδοιπόροι σε μια χωρίς προηγούμενο μαθηματική εκστρατρεία, όπως είναι αυτή που βιώνουμε σε αυτή την ιστοσελίδα.Η εμπειρία που θα αποκομίσουν θα τους συνοδεύει σε όλη τους τη ζωή.

Μπάμπης

NAI - NAI - NAI - NAI
Και ας μή ξεχνάμε, ότι οι επί σειρά ετών Άριστοι και Tροπαιούχοι μας τιμούν με τη παρουσία τους και τη συμμετοχή τους εδώ στην οικογένεια mathematica, τόσο πρίν όσο και μετά τις επιτυχίες τους.

S.E.Louridas

#48

Πολλά συγχαρητήρια και από εμένα σε όλους τους διακριθέντες αλλά και σε όλους τους συμμετέχοντες. Να μην ξεχνάμε ότι η συμμετοχή είναι σημαντική εμπειρία και ότι πρωτίστως το ζητούμενο είναι μάλλον η χαρά που αποκομίζει ο διαγωνιζόμενος από την όλη διαδικασία και δευτερευόντως η διάκριση.

leonidas 1 · #49

Θα συμφωνήσω ΠΑΡΑ ΠΟΛΥ με την πρόταση του Κ Στεργίου και πρέπει να μελετηθεί σοβαρά.
Είναι κρίμα παιδιά Β Γυμνασίου να υφίστανται την ταλαιπωρία της μετάβασης στην Αθήνα και τα συνακόλουθα έξοδα (που για μια μέση οικογένεια είναι ένα σεβαστό
ποσό) χωρίς οι περισσότεροι να γνωρίζουν ότι αυτό που θα μείνει στο παιδί τους είναι η απογοήτευση.
Και με την ευκαιρία(αν και δεν είναι θέμα που αφορά το mathematica) θα παρακαλούσα κάποιον της Ε.Μ.Ε να διαλύσει τις σκιές απο τις φήμες ότι
α) Σε παραρτήματα οι βαθμολογητές παίρνουν τα γραπτά στο σπίτι τους .
β)Οτι υπάρχει μόνο μία βαθμολόγηση .
γ)Οτι επιτηρητές ή βαθμολογητές είναι και άτομα που κάνουν ιδιαίτερα μαθήματα για διαγωνισμούς.
Ελπίζω να μην απαντήσει μόνο ο Γιάννης Κερασαρίδης αν και θα είχε ιδιαίτερη βαρύτητα η τοποθέτηση του Κ.Λουρίδα

#50

Δε θα μπορούσα παρά να συγχαρώ όλους τους συμμετέχοντες και από τους διακριθέντες όλα τα μέλη μας!!

Παιδιά μας κάνετε υπερήφανους...

Τελειώνω το μήνυμα με μία πολύ απλή λύση στο θέμα της Γεωμετρίας των μικρών (του συναδέλφου Φραγκίσκου Τζωρτζακάκη από τους Βόρους Ηρακλείου που έδινε ο γιος του ο Ανδρέας στον Αρχιμήδη). Το σχήμα είναι του Θανάση Μπεληγιάννη από προηγούμενη δημοσίευσή του.

Είναι AE=AB

άρα $\angle{E\Gamma A}=\angle{A\Gamma \Delta} \ \ (1)$

Επίσης $\angle{AB\Delta}=\angle{A\Delta B}$ οπότε από το εγγράψιμο τετράπλευρο $AB\Gamma E$ οι παραπληρωματικές τους είναι ίσες δηλαδή $\angle{AE\Gamma}=\angle{A\Delta\Gamma} \ \ (2)$ .

: ARXIMIDIS.png (21.34 KiB) Προβλήθηκε 3347 φορές

Από τις

και τα τρίγωνα $A\Delta \Gamma, AE\Gamma$ προκύπτει τελικά ότι $\angle{DA\Gamma}=\angle{\Gamma A E}$ που είναι και το ζητούμενο.

Αλέξανδρος

S.E.Louridas · #51

leonidas 1 έγραψε:Θα συμφωνήσω ΠΑΡΑ ΠΟΛΥ με την πρόταση του Κ Στεργίου και πρέπει να μελετηθεί σοβαρά.
Είναι κρίμα παιδιά Β Γυμνασίου να υφίστανται την ταλαιπωρία της μετάβασης στην Αθήνα και τα συνακόλουθα έξοδα (που για μια μέση οικογένεια είναι ένα σεβαστό
ποσό) χωρίς οι περισσότεροι να γνωρίζουν ότι αυτό που θα μείνει στο παιδί τους είναι η απογοήτευση.
Και με την ευκαιρία(αν και δεν είναι θέμα που αφορά το mathematica) θα παρακαλούσα κάποιον της Ε.Μ.Ε να διαλύσει τις σκιές απο τις φήμες ότι
α) Σε παραρτήματα οι βαθμολογητές παίρνουν τα γραπτά στο σπίτι τους .
β)Οτι υπάρχει μόνο μία βαθμολόγηση .
γ)Οτι επιτηρητές ή βαθμολογητές είναι και άτομα που κάνουν ιδιαίτερα μαθήματα για διαγωνισμούς.
Ελπίζω να μην απαντήσει μόνο ο Γιάννης Κερασαρίδης αν και θα είχε ιδιαίτερη βαρύτητα η τοποθέτηση του Κ.Λουρίδα

Προσωπικά δηλώνω κατηγορηματικά, και μετά λόγου γνώσεως ότι το αδιάβλητο της βαθμολογίας αλλά και της διαφύλαξης των θεμάτων είναι δεδομένα εδώ και δεκαετίες παρ' όλo που στηρίζονται περισσότερο στην ηθική αντίληψη των πραγμάτων και λιγότερο στους τύπους.
Αρνητικά θα μπορούσαμε να αναζητήσουμε σε άλλα πράγματα, όχι όμως σε αυτά.

S.E.Louridas

kalagz · #52

Να ευχηθώ κι εγώ με τη σειρά μου (τώρα που γύρισα στον υπολογιστή μου!

) ΣΥΓΧΑΡΗΤΗΡΙΑ ΣΕ ΟΛΟΥΣ ΤΟΥΣ ΔΙΑΚΡΙΘΕΝΤΕΣ!ΚΑΙ ΚΑΛΗ ΣΥΝΕΧΕΙΑ ΣΤΟΥΣ ΔΙΑΓΩΝΙΣΜΟΥΣ!.
Αναφέρω τώρα άλλη μια λύση της Γεωμετρίας των μεγάλων που βρήκα στο γυρισμό προς Πάτρα. Μάλιστα, χωρίς τη χρήση λημμάτων, για να μή λένε μερικοί....!

Έστω ότι η

τέμνει την

στο

και την

στο

. Θα δείξω ότι τα D,N,T

είναι συνευθειακά. Θεωρούμε την ομοιοθεσία με κέντρο

και λόγο $\lambda = \frac{AO}{AO_1}$ . Αυτή στέλνει τον κύκλο (O_1,O_A)

στον

και τα σημεία E,D,Z,H

στα

αντίστοιχα.
Έτσι $\lambda=\frac{AB}{AE} = \frac{AC}{AZ} = \frac{AD}{AH} = \frac{AK}{AD}$ .
Από το θεώρημα Μενελάου για το τρίγωνο AKC

και τα σημεία H,Z,T

παίρνουμε $\frac{AH}{HK} \cdot \frac{KT}{TC} \cdot \frac{CZ}{ZA} =1$ . Άρα $\frac{KT}{TC} = \frac{AZ}{ZC} \cdot \frac{HK}{HA}$ .
τους οποίους λόγους μπορούμε να τους βρούμε μόνο ως προς $\lambda$ .
Για να διέρχεται τώρα και η

από το ίδιο σημείο, σύμφωνα με το αντίστροφο του θ. Μενελάου θα πρέπει $\frac{AD}{DK} \cdot \frac{KT}{ST} \cdot \frac{CM}{MA} =1$ , κάτι το οποίο προκύπτει αν χρησιμοποιήσουμε την ομοιοθεσία για να βρούμε τους λόγους ως προς $\lambda$ . Πιο αναλυτικα:
$\frac{AC}{AZ}= \lambda \Rightarrow \frac{AC-AZ}{AZ}= \lambda-1 \Rightarrow \frac{AZ}{ZC}= \frac{\lambda}{\lambda-1}$
$\frac{AC}{AZ}=\lambda \Rightarrow \frac{AC}{AC-AZ}=\frac{\lambda}{\lambda-1} \Rightarrow \frac{AM+MC}{2MC}=\frac{\lambda}{\lambda-1} \Rightarrow \frac{AM}{MC}= \frac{\lambda+1}{\lambda-1}$
$\frac{AD}{DK}=\frac{AD}{AK-AD}=\frac{1}{\lambda-1}$
$\frac{HK}{HA}=\frac{AK-AH}{AH}=\frac{AK}{AH}-1= \frac{AK}{AD} \cdot \frac{AD}{AH} -1 = \lambda^2-1$ .
Συνδυάζοντας τις παραπάνω σχέσεις προκύπτει το ζητούμενο!

Αντίστοιχα αποδεικνύουμε ότι η

διέρχεται από το σημείο τομής των

και

.

Για τη μεσοκάθετο, θα πρέπει προφανώς η

να είναι κάθετη στην

. Όμως είναι κάθετη στη

οπότε θα πρέπει $BC \parallel EZ$ . Με λίγο
ψάξιμο στις γωνίες βλέπουμε ότι το AHCT

θα πρέπει να είναι εγγράψιμο. Αυτό προκύπτει από τα όμοια τρίγωνα AEH

και

. Συνεπώς το
BCTS

είναι ισοσκελές τραπέζιο κλπ κλπ!

: Arximidis2012-P3.png (40.38 KiB) Προβλήθηκε 3198 φορές

Το φετινά θέματα μου άρεσαν πολύ, θεωρώ ότι όλα ήταν "από λίγο" δύσκολα.Βέβαια, άλλη μια φορά η γεωμετρία είχε 6 "συντρεχικότητες"...

ΥΓ:Ελπίζω αυτή τη φορά να μη διαγραφεί η απάντηση μου.

ΑΡΣΕΝΟΗ · #53

Kαι το τέταρτο θέμα τον μικρών:

Πάνω σε επίπεδο $\Pi$ δίνεται ευθεία $\epsilon$ και πάνω στην $\epsilon$ δίνονται δύο σημεία $A_{1},A_{2},$ διαφορετικά μεταξύ τους. Θεωρούμε ακόμη και δύο διαφορετικά μεταξύ τους σημεία $A_{3}, A_{4}$ του επιπέδου $\Pi$ , που δεν ανήκουν στη ευθεία $\epsilon$ .Να εξετάσετε, αν είναι δυνατόν να τοποθετηθούν τα σημεία $A_{3}$ και $A_{4}$ σε τέτοιες Θέσεις, ώστε να σχηματίζεται ο μεγαλύτερος δυνατός αριθμός ισοσκελών τριγώνων με κορυφές τρία απο τα τέσσερα σημεία $A_{1}, A_{2} , A_{3}, A_{4}$ :
(α)όταν τα σημεία $A_{3},A_{4}$ ανήκουν σε διαφορετικά ημιεπίπεδα ως προς την ευθεία $\epsilon$
(β)όταν τα σημεία $A_{3},A_{4}$ ανήκουν στο ίδιο ημιεπίπεδο ως προς την ευθεία $\epsilon$

#54

Δίνω και εγώ μια απλή λύση για την γεωμετρία των μικρών, χρησιμοποιόντας το σχήμα του Αλέξανδρου (Cretanmann) λίγο πιο πάνω:

Η γωνία $\displaystyle{EA\Gamma ,}$ είναι ίση με την $\displaystyle{EB\Gamma ,}$ ως εγγεγραμμένες που βαίνουν στο ίδιο τόξο. Η γωνία
$\displaystyle{\Delta AE}$ είναι επίκεντρη και η γωνία $\displaystyle{EB\Delta ,}$ είναι εγγεγραμμένη και βαίνει στο ίδιο τόξο. Άρα
$\displaystyle{EA\Delta =2EB\Delta \Rightarrow A_{1}+\theta =2\theta \Rightarrow A_{1}=\theta .}$

S.E.Louridas · #55

Πράγματι το θέμα της Γεωμετρίας των Μεγάλων δίνει τη δυνατότητα για λύσεις (ποικιλία).

Να λοιπόν και μία λύση «θύραθεν» που μετά από σκέψη για το άν θα έπρεπε να την παραθέσω, τελικά τη παραθέτω.

$DZ{'} \parallel KC,DE{'} \parallel KB \Rightarrow E{'} Z{'} \parallel BC \Rightarrow AE{'} DZ{'} \sim ABKC,\;\dot \alpha \rho \alpha \;\tau o\;AE{'} DZ{'}$
είναι εγγεγραμμένο στον πράσινο κύκλο με κέντρο στην AO.

Λόγω του μονοσήμαντου αυτός είναι ο της εκφώνησης οπότε:
$Z \equiv Z{'} ,E \equiv E{'} ,T \equiv T{'} ,\Sigma \equiv \Sigma {'} .$
Επειδή οι διαγώνιοι παραλληλογράμμου διχοτομούνται (αναφερόμαστε στα παραλληλόγραμμα $BDE\Sigma ,\;DCTZ$ ) το πρόβλημα θεωρώ ότι λύθηκε.

S.E.Louridas

Karanus · #56

Η πολύ συντομη και απλή λύση του ΔΗΜΗΤΡΗ (με σχολική ύλη μόλις Β γυμνασίου και ούτε,χρησιμοποιεί όλο και όλο το στοιχειώδες θεώρημα της εγγεγραμμένης), μας δείχνει ότι καμιά φορά ασχολούμαστε με πάρα πολύ δύσκολα θέματα με αποτέλεσμα να σκεφτόμαστε περίπλοκα και χάνουμε τα εύκολα μέσα απο τα χέρια μας.....

#57

S.E.Louridas έγραψε:
leonidas 1 έγραψε:Θα συμφωνήσω ΠΑΡΑ ΠΟΛΥ με την πρόταση του Κ Στεργίου και πρέπει να μελετηθεί σοβαρά.
Είναι κρίμα παιδιά Β Γυμνασίου να υφίστανται την ταλαιπωρία της μετάβασης στην Αθήνα και τα συνακόλουθα έξοδα (που για μια μέση οικογένεια είναι ένα σεβαστό
ποσό) χωρίς οι περισσότεροι να γνωρίζουν ότι αυτό που θα μείνει στο παιδί τους είναι η απογοήτευση.
Και με την ευκαιρία(αν και δεν είναι θέμα που αφορά το mathematica) θα παρακαλούσα κάποιον της Ε.Μ.Ε να διαλύσει τις σκιές απο τις φήμες ότι
α) Σε παραρτήματα οι βαθμολογητές παίρνουν τα γραπτά στο σπίτι τους .
β)Οτι υπάρχει μόνο μία βαθμολόγηση .
γ)Οτι επιτηρητές ή βαθμολογητές είναι και άτομα που κάνουν ιδιαίτερα μαθήματα για διαγωνισμούς.
Ελπίζω να μην απαντήσει μόνο ο Γιάννης Κερασαρίδης αν και θα είχε ιδιαίτερη βαρύτητα η τοποθέτηση του Κ.Λουρίδα

Προσωπικά δηλώνω κατηγορηματικά, και μετά λόγου γνώσεως ότι το αδιάβλητο της βαθμολογίας αλλά και της διαφύλαξης των θεμάτων είναι δεδομένα εδώ και δεκαετίες παρ' όλo που στηρίζονται περισσότερο στην ηθική αντίληψη των πραγμάτων και λιγότερο στους τύπους.
Αρνητικά θα μπορούσαμε να αναζητήσουμε σε άλλα πράγματα, όχι όμως σε αυτά.

S.E.Louridas

Συμφωνώ με τον Σωτήρη και:δηλώνω και εγώ ΚΑΤΗΓΟΡΗΜΑΤΙΚΑ ως πρόεδρος της επιτροπής για τους διαγωνισμούς ΘΑΛΗΣ και ΕΥΚΛΕΙΔΗΣ επί σειρά ετών, στην επαρχιακή πόλη της Ιστιαίας Ευβοίας όπου δίνουν εξετάσεις οι μαθητές από την Βόρεια Εύβοια, ότι οι εξετάσεις είναι ΠΛΗΡΩΣ ΑΔΙΑΒΛΗΤΕΣ, τα δε γραπτά, αποστέλλονται αμέσως μετά το πέρας των εξετάσεων στην ΕΜΕ με Courier. Οποιαδήποτε επέμβαση εξ άλλου από τον υπεύθυνο καθηγητή σε γραπτά μαθητών, θα γελοιοποιούσε τον ίδιο και σε τίποτε δεν θα ωφελούσε τον μαθητή...

Ιωάννου Δημήτρης

mathfinder · #58

Το 4ο ΘΕΜΑ των "ΜΕΓΑΛΩΝ "
Το ισοσκελές τραπέζιο του σχήματος αποτελείται από ίσα μεταξύ τους ισόπλευρα τρίγωνα που οι πλευρές τους έχουν μήκος 1 . Η πλευρά $A_{1}E$ έχει μήκος

και η μεγάλη βάση του $A_{1}A_{\nu }$ έχει μήκος $\nu -1$ . Ξεκινάμε από το σημείο $A_{1}$ και κινούμαστε κατά μήκος των ευθυγράμμων τμημάτων που ορίζονται μόνο προς τα δεξιά και επάνω (λοξά αριστερά ή λοξά δεξιά) . Υπολογίστε (συναρτήσει του $\nu$ ή ανεξάρτητα από αυτό ) το πλήθος όλων των δυνατών διαδρομών που μπορούμε να ακολουθήσουμε , με σκοπό να καταλήξουμε στα σημεία $B,\Gamma ,\Delta ,E$ , όπου $\nu$ ακέραιος μεγαλύτερος του

.

Kostas_94 · #59

mathfinder έγραψε:Το 4ο ΘΕΜΑ των "ΜΕΓΑΛΩΝ "
Το ισοσκελές τραπέζιο του σχήματος αποτελείται από ίσα μεταξύ τους ισόπλευρα τρίγωνα που οι πλευρές τους έχουν μήκος 1 . Η πλευρά $A_{1}E$ έχει μήκος και η μεγάλη βάση του $A_{1}A_{\nu }$ έχει μήκος $\nu -1$ . Ξεκινάμε από το σημείο $A_{1}$ και κινούμαστε κατά μήκος των ευθυγράμμων τμημάτων που ορίζονται μόνο προς τα δεξιά και επάνω (λοξά αριστερά ή λοξά δεξιά) . Υπολογίστε (συναρτήσει του $\nu$ ή ανεξάρτητα από αυτό ) το πλήθος όλων των δυνατών διαδρομών που μπορούμε να ακολουθήσουμε , με σκοπό να καταλήξουμε στα σημεία $B,\Gamma ,\Delta ,E$ , όπου $\nu$ ακέραιος μεγαλύτερος του .

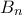Έστω $B_{n}, C_{n}, D_{n}$ τα σημεία της 2ης, 3ης, 4ης σειράς. Σε κάθε σημείο αντιστοιχίζουμε τους τρόπους με τους οποίους μπορούμε να φτάσουμε μέχρι εκεί με την καθορισμένη διαδικασία. Προφανώς $A_{n}=1$ . Για τις επόμενες τρεις ακολουθίες θα χρησιμοποιήσουμε αναδρομικούς τύπους. Έτσι προκειμένου να βρούμε π.χ το $B_{n}$ , αρκεί να προσθέσουμε τους δυνατούς τρόπους με τους οποίους φτάνουμε στα 3 πιθανά προηγούμενα σημεία. Δηλαδή $B_{n}=B_{n-1}+A_{n}+A_{n+1}=B_{n-1}+2$ , με $B_{1}=2$ , οπότε είναι αριθμητική πρόοδος και προφανώς $B_{n}=2n$ . Ομοίως
$C_{n}=C_{n-1}+B_{n}+B_{n+1}$
$C_{n-1}=C_{n-2}+B_{n-1}+B_{n}$
. . . . .
$C_{1}=B_{1}+B_{2}=6$
Προσθέτοντας κατά μέλη, είναι
$\displaystyle{C_{n}= 6+2\sum_{i=1}^{n+1}{B_{i}}-2B_{1}-B_{2}-B_{n+1}=-2-2(n+1)+4\sum_{i=1}^{n+1}{i}=-2-2(n+1)+2(n+1)(n+2)=2(n+1)^2-2$ .
Τέλος έχουμε
$D_{n}=D_{n-1}+C_{n}+C_{n+1}$
$D_{n-1}=D_{n-2}+C_{n-1}+C_{n}$
. . . . .
$D_{1}=C_{2}+C_{1}=6+16=22(=E)$
Προσθέτοντας κατά μέλη, είναι
$\displaystyle{D_{n}=22-2C_{1}-C_{2}-C_{n+1}+2\sum_{i=1}^{n+1}{C_{i}}=22-12-16-2(n+2)^2+2+\sum_{i=2}^{n+1}{(2(i+1)^2-2)}=}$
$\displaystyle{-8-2(n+2)^2-4(n+1)+4\sum_{i=1}^{n+2}{i^2}=-8-2(n+2)^2-4(n+1)+\frac{2}{3}(n+2)(n+3)(2n+5)}(1)$
Για να βρούμε τα σημεία που ζητάει, αρκεί να υπολογίσουμε με βάση τους τύπους που βρήκαμε:
E=22

$B=B_{\nu-1}=2\nu-2$
$C=C_{\nu-2}=2(\nu-1)^2-2=2\nu(\nu-2)$
$D=D_{\nu-3}$ , όσο βγαίνει από το (1)
Ίσως υπάρχει και πολύ πιο σύντομη λύση, γιατί όπως συνήθως οι αναδρομικες σχέσεις απαιτούν πολλές πράξεις. Οι τύποι πάντως νομίζω οτι είναι σωστοί, γιατί φαίνεται να επαληθεύουν τις μικρές τιμές.

slash · #60

Να ευχηθώ και ΄γω συγχαρητήρια σε όλους όσους συμμετείχαν. Προσωπικά φέτος ήθελα απλά να φτάσω μέχρι τον αρχιμήδη καθώς ασχολούμαι λίγο περισσότερο απο 1 χρόνο με τα μαθηματικά, αλλά αφού έτυχε ...

Βασικά θα ήθελα να ρωτήσω που θα μπορούσα να βρώ παλιά θέματα προκριματικών διαγωνισμών.

Καλή συνέχεια να έχουμε στον προκριματικό !

Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Re: Αρχιμήδης Καλή επιτυχία.

Μέλη σε σύνδεση