1. α) Από την
 ενός τόξου
ενός τόξου  να υπολογισθούν οι τριγωνομετρικοί αριθμοί ημίτονο, συνημίτονο του τόξου
να υπολογισθούν οι τριγωνομετρικοί αριθμοί ημίτονο, συνημίτονο του τόξου  .
.β) Αν
 και
και  και
και  να υπολογίσετε το
να υπολογίσετε το  .
.2. α) Σε δοθέντα κύκλο
 να εγγράψετε κανονικό εξάγωνο και να υπολογίσετε την πλευρά και το απόστημά του από την ακτίνα του κύκλου.
να εγγράψετε κανονικό εξάγωνο και να υπολογίσετε την πλευρά και το απόστημά του από την ακτίνα του κύκλου.β) Δίνεται το ισοσκελές τρίγωνο
 . Από την κορυφή
. Από την κορυφή  αυτού φέρουμε την
αυτού φέρουμε την  κάθετη στο επίπεδο του τριγώνου
κάθετη στο επίπεδο του τριγώνου και ενώνουμε το τυχόν σημείο
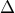 της
της  με το μέσο
με το μέσο  της βάσεως
της βάσεως  . Να αποδειχθεί ότι είναι :
. Να αποδειχθεί ότι είναι : i)
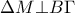
ii)
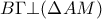 .
.3. α) Δείξτε ότι κάθε μιγαδικός αριθμός μπορεί να γραφεί σαν τετράγωνο μιγαδικού αριθμού.
β) Αν
 , να δείξετε ότι
, να δείξετε ότι 
γ) Αν
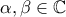 τότε σύμφωνα με την ερώτηση (α) υπάρχει ένα
τότε σύμφωνα με την ερώτηση (α) υπάρχει ένα  τέτοιο ώστε
τέτοιο ώστε 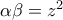 .
. Αποδείξτε την ισότητα
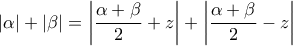 .
.4. α) Δείξτε ότι το σύνολο
 των ριζών της εξίσωσης
των ριζών της εξίσωσης  είναι ομάδα με πράξη τον πολλαπλασιασμό στο σύνολο
είναι ομάδα με πράξη τον πολλαπλασιασμό στο σύνολο  .
.β) Δείξτε ότι δυο οποιεσδήποτε από τις ρίζες της προηγούμενης εξισώσεως είναι γραμμικώς ανεξάρτητα στοιχεία του διανυσματικού χώρου
 πάνω στο
πάνω στο  .
.
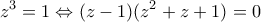 , βρίσκουμε ότι:
, βρίσκουμε ότι: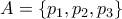 , όπου
, όπου 
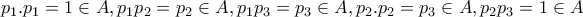 και
και 

 είναι
είναι  , διότι
, διότι  , το συμμετρικό του
, το συμμετρικό του 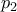 είναι το
είναι το  , αφού
, αφού 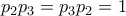 και το
και το  είναι ομάδα (και μάλιστα αβελιανή, αφού προφανώς ισχύει και η αντιμεταθετική ιδιότητα)
είναι ομάδα (και μάλιστα αβελιανή, αφού προφανώς ισχύει και η αντιμεταθετική ιδιότητα) του
του  με
με  . Τότε:
. Τότε:

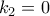
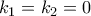 και άρα έχουμε το ζητούμενο.
και άρα έχουμε το ζητούμενο. είναι γραμμικώς ανεξάρτητα.
είναι γραμμικώς ανεξάρτητα. είναι και αυτά γραμμικώς ανεξάρτητα.
είναι και αυτά γραμμικώς ανεξάρτητα.
 και
και 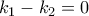
 . Θα αποδείξουμε ότι υπάρχει
. Θα αποδείξουμε ότι υπάρχει  , ώστε
, ώστε 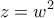
 . Τότε
. Τότε  . Οπότε αν
. Οπότε αν 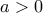 , τότε
, τότε  . Eνώ αν
. Eνώ αν  , τότε
, τότε . Άρα στην πρώτη περίπτωση έχουμε το ζητούμενο.
. Άρα στην πρώτη περίπτωση έχουμε το ζητούμενο. . Τότε
. Τότε 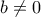 . Έστω λοιπόν
. Έστω λοιπόν  . Θέλουμε να βρούμε τους αριθμούς
. Θέλουμε να βρούμε τους αριθμούς  και
και 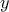 , ώστε να είναι
, ώστε να είναι 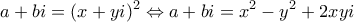 . Άρα πρέπει:
. Άρα πρέπει: και
και
 . Άρα από την δεύτερη εξίσωση του πιο πάνω συστήματος, παίρνουμε
. Άρα από την δεύτερη εξίσωση του πιο πάνω συστήματος, παίρνουμε και τότε η πρώτη εξίσωση γράφεται:
και τότε η πρώτη εξίσωση γράφεται: 
 . Και αν θέσουμε
. Και αν θέσουμε 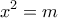 , έχουμε
, έχουμε 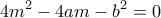
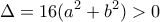 , (εφ όσον είναι
, (εφ όσον είναι  . Αυτό σημαίνει ότι υπάρχει μία ρίζα
. Αυτό σημαίνει ότι υπάρχει μία ρίζα  της εξίσωσης που είναι θετική.
της εξίσωσης που είναι θετική. , ή
, ή 
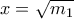 , τότε θα είναι
, τότε θα είναι 
 και το ζητούμενο εδείχθη.
και το ζητούμενο εδείχθη.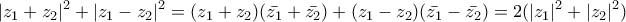
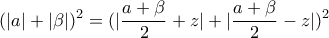 , ή
, ή

 , ή
, ή , το οποίο αληθεύει , λόγω του (β) ερωτήματος.
, το οποίο αληθεύει , λόγω του (β) ερωτήματος. , και
, και 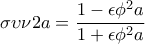 , (Θεωρία)
, (Θεωρία)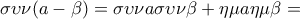
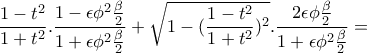
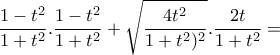
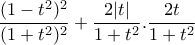 .
. . Άρα
. Άρα  , οπότε έχουμε:
, οπότε έχουμε:
 , θα είναι κάθετη προς κάθε ευθεία αυτού.
, θα είναι κάθετη προς κάθε ευθεία αυτού.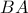 και
και  . Συνεπώς τα ορθογώνια τρίγωνα
. Συνεπώς τα ορθογώνια τρίγωνα  και
και  είναι ίσα αφού έχουν επί πλέον την
είναι ίσα αφού έχουν επί πλέον την  κοινή και
κοινή και  .
.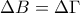 και άρα το τρίγωνο
και άρα το τρίγωνο 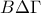 είναι ισοσκελές και άρα η
είναι ισοσκελές και άρα η  , θα είναι και ύψος.
, θα είναι και ύψος. είναι κάθετη προς δύο τεμνόμενες ευθείες του επιπέδου
είναι κάθετη προς δύο τεμνόμενες ευθείες του επιπέδου  , τις
, τις  και
και 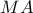

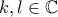 ώστε
ώστε  οπότε
οπότε 
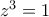 ἀποτελοῦν ὁμάδα, ὡς πρός τόν πολλαπλασιασμό:
ἀποτελοῦν ὁμάδα, ὡς πρός τόν πολλαπλασιασμό: