 , με
, με 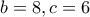 , ο εγγεγραμμένος κύκλος
, ο εγγεγραμμένος κύκλος  , εφάπτεται
, εφάπτεται των πλευρών
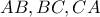 στα σημεία
στα σημεία 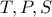 αντίστοιχα . Φέρουμε τμήμα :
αντίστοιχα . Φέρουμε τμήμα :  .
.Βρείτε τον λόγο :
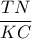 . Μπορείτε να κάνετε το ίδιο για οποιαδήποτε μήκη των πλευρών
. Μπορείτε να κάνετε το ίδιο για οποιαδήποτε μήκη των πλευρών 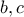 ;
;Συντονιστές: AΝΔΡΕΑΣ ΒΑΡΒΕΡΑΚΗΣ, silouan, george visvikis
 , με
, με 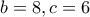 , ο εγγεγραμμένος κύκλος
, ο εγγεγραμμένος κύκλος  , εφάπτεται
, εφάπτεται 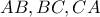 στα σημεία
στα σημεία 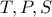 αντίστοιχα . Φέρουμε τμήμα :
αντίστοιχα . Φέρουμε τμήμα :  .
.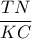 . Μπορείτε να κάνετε το ίδιο για οποιαδήποτε μήκη των πλευρών
. Μπορείτε να κάνετε το ίδιο για οποιαδήποτε μήκη των πλευρών 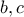 ;
;To κάνω με κάμποση Τριγωνομετρία, αλλά γίνεται και χωρίς.
 η ακτίνα του εγγεγραμμένου κύκλου, τότε
η ακτίνα του εγγεγραμμένου κύκλου, τότε 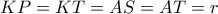 . Επίσης εύκολα βλέπουμε ότι η
. Επίσης εύκολα βλέπουμε ότι η 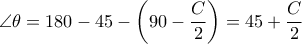
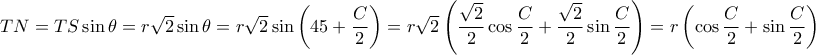
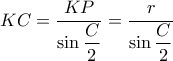
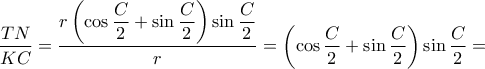
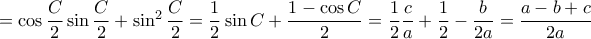
Προφανώς τα σημεία
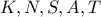 είναι ομοκυκλικά και μπλε γωνίες ίσες.
είναι ομοκυκλικά και μπλε γωνίες ίσες.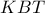 η μπλε κι η κόκκινη είναι συπληρωματικές ,τα σημεία
η μπλε κι η κόκκινη είναι συπληρωματικές ,τα σημεία 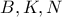 είναι συνευθειακά κι έστω
είναι συνευθειακά κι έστω 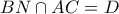
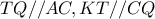 άρα
άρα 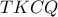 παραλ/μμο ,άρα
παραλ/μμο ,άρα 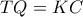
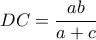
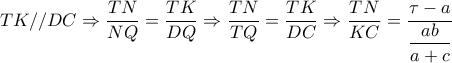
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 2 επισκέπτες