ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Συνάδελφοι γεια σας !
Διαπιστώνω με χαρά ότι είστε όλοι σχεδόν ευχαριστημένοι με τα σημερινά θέματα και έτσι πρέπει να είναι .Η επιτροπή τα πήγε πολύ καλά και τα θέματα ήταν κοντά στις προσδοκίες των μελών μας μια και ανταποκρίνονται στο κύριο αίτημα του mathematica , σύμφωνα με το οποίο :
'' .....η επιτροπή , μεταξύ των άλλων , πρέπει να προτείνει ωραία, σωστά δομημένα και ευρέως αποδεκτά θέματα , που να είναι αντάξια των προσδοκιών της μαθηματικής κοινότητας , αλλά και ανάλογα του τεράστιου αγώνα που κάνουν οι μαθητές, οι γονείς τους αλλά και μεις ως δάσκαλοι, ανεξάρτητα από το μετερίζι που πολεμάμε. ''
(δείτε σχετικό θέμα : viewtopic.php?f=6&t=1183)
Με το μήνυμα αυτό θέλω να σας προτρέψω να συμβάλουμε όλοι μας , ως μαθηματικοί αλλά και ως δάσκαλοι , στην σωστή βαθμολόγηση των γραπτών. Αυτό βέβαια είναι έργο των βαθμολογητών και των συντονιστών τους, αλλά το mathematica με την μεγάλη απήχηση που έχει μπορεί να συμβάλλει σημαντικά στο εξής σημείο :
Να συγκεντρώσει στο χώρο αυτό όσο δυνατόν περισσότερες εναλλακτικές λύσεις στα τρία ζητήματα των ασκήσεων, για να φτάσουν γρήγορα στους βαθμολογητές.Κάθε ένας μας λοιπόν που είτε ο ίδιος είτε οι μαθητές του είτε συνάδελφός του έχει κάνει διαφορετική λύση σε κάποιο υποερώτημα, ας το γράψει σε ένα αρχείο word και να το στείλει συνημμένο στο χώρο αυτό. Σκοπεύω να μαζέψω όλα αυτά τα αρχεία , να τα κάνω ένα ολοκληρωμένο εννιαίο αρχείο , ανά θέμα , και στη συνέχεια να το στείλλω σε όλα τα βαθμολογικά κέντρα της χώρας μας.Το υπουργείο φέτος έχει κάνει ένα σημαντικό βήμα και δίνει τη δυνατότητα στους συντονιστές να επικοινωνούν μεταξύ τους σε ειδική ιστοσελίδα, να συζητούν , να ανταλλάσσουν απόψεις , λύσεις , μοριοδοτήσεις κλπ οπότε είναι μεγάλη ευκαιρία να συμβάλλουμε θετικά στην ακόμα καλύτερη αξιολόγηση των γραπτών.
Συνάδελφοι , μια τέτοια προσπάθεια θα προβάλει ακόμα περισσότερο το mathematica αλλά και εσείς θα νοιώθετε την ικανοποίηση ότι κάνατε τα δέοντα για την επιτυχία των μαθητών σας μέχρι την ύστατη στιγμή. Σκεφτείτε ότι θα είναι κρίμα μια έξυπνη και πρωτότυπη λύση μαθητή σας να ...ξεγλιστρήσει από τα μάτια των συναδέλφων βαθμολογητών και να χαθούν άσκοπα μόρια. Ήδη έχω δεχθεί τηλεφωνήματα από συναδέλφους που επιθυμούν να μου στείλλουν διαφορετικές λύσεις και να φτάσουν στους αποδέκτες , ώστε και εκείνοι να βοηθηθούν στο τόσο δύσκολο, υπεύθυνο και αγωνιώδες έργο τους.
Με ευχαρίστηση θα δεχτώ τυχόν συμπληρωματικές παρατηρήσεις σας .
Μπάμπης
Διαπιστώνω με χαρά ότι είστε όλοι σχεδόν ευχαριστημένοι με τα σημερινά θέματα και έτσι πρέπει να είναι .Η επιτροπή τα πήγε πολύ καλά και τα θέματα ήταν κοντά στις προσδοκίες των μελών μας μια και ανταποκρίνονται στο κύριο αίτημα του mathematica , σύμφωνα με το οποίο :
'' .....η επιτροπή , μεταξύ των άλλων , πρέπει να προτείνει ωραία, σωστά δομημένα και ευρέως αποδεκτά θέματα , που να είναι αντάξια των προσδοκιών της μαθηματικής κοινότητας , αλλά και ανάλογα του τεράστιου αγώνα που κάνουν οι μαθητές, οι γονείς τους αλλά και μεις ως δάσκαλοι, ανεξάρτητα από το μετερίζι που πολεμάμε. ''
(δείτε σχετικό θέμα : viewtopic.php?f=6&t=1183)
Με το μήνυμα αυτό θέλω να σας προτρέψω να συμβάλουμε όλοι μας , ως μαθηματικοί αλλά και ως δάσκαλοι , στην σωστή βαθμολόγηση των γραπτών. Αυτό βέβαια είναι έργο των βαθμολογητών και των συντονιστών τους, αλλά το mathematica με την μεγάλη απήχηση που έχει μπορεί να συμβάλλει σημαντικά στο εξής σημείο :
Να συγκεντρώσει στο χώρο αυτό όσο δυνατόν περισσότερες εναλλακτικές λύσεις στα τρία ζητήματα των ασκήσεων, για να φτάσουν γρήγορα στους βαθμολογητές.Κάθε ένας μας λοιπόν που είτε ο ίδιος είτε οι μαθητές του είτε συνάδελφός του έχει κάνει διαφορετική λύση σε κάποιο υποερώτημα, ας το γράψει σε ένα αρχείο word και να το στείλει συνημμένο στο χώρο αυτό. Σκοπεύω να μαζέψω όλα αυτά τα αρχεία , να τα κάνω ένα ολοκληρωμένο εννιαίο αρχείο , ανά θέμα , και στη συνέχεια να το στείλλω σε όλα τα βαθμολογικά κέντρα της χώρας μας.Το υπουργείο φέτος έχει κάνει ένα σημαντικό βήμα και δίνει τη δυνατότητα στους συντονιστές να επικοινωνούν μεταξύ τους σε ειδική ιστοσελίδα, να συζητούν , να ανταλλάσσουν απόψεις , λύσεις , μοριοδοτήσεις κλπ οπότε είναι μεγάλη ευκαιρία να συμβάλλουμε θετικά στην ακόμα καλύτερη αξιολόγηση των γραπτών.
Συνάδελφοι , μια τέτοια προσπάθεια θα προβάλει ακόμα περισσότερο το mathematica αλλά και εσείς θα νοιώθετε την ικανοποίηση ότι κάνατε τα δέοντα για την επιτυχία των μαθητών σας μέχρι την ύστατη στιγμή. Σκεφτείτε ότι θα είναι κρίμα μια έξυπνη και πρωτότυπη λύση μαθητή σας να ...ξεγλιστρήσει από τα μάτια των συναδέλφων βαθμολογητών και να χαθούν άσκοπα μόρια. Ήδη έχω δεχθεί τηλεφωνήματα από συναδέλφους που επιθυμούν να μου στείλλουν διαφορετικές λύσεις και να φτάσουν στους αποδέκτες , ώστε και εκείνοι να βοηθηθούν στο τόσο δύσκολο, υπεύθυνο και αγωνιώδες έργο τους.
Με ευχαρίστηση θα δεχτώ τυχόν συμπληρωματικές παρατηρήσεις σας .
Μπάμπης
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Μπάμπη καλησπέρα.
Στο θέμα 3Βγ μια ωραία λύση που έδωσε μαθητής μου είναι η εξής:
Βρήκε το όρια \displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}
\displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = + \infty και
και  \displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}
\displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = - \infty οπότε ....
οπότε ....
Θωμάς
Στο θέμα 3Βγ μια ωραία λύση που έδωσε μαθητής μου είναι η εξής:
Βρήκε το όρια
 \displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}
\displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = + \infty
 και
και  \displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}
\displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = - \infty
 οπότε ....
οπότε ....Θωμάς
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Θωμά, ευχαριστώ ! Δεν τη στέλνεις και σε word για να την έχω έτοιμη ; Την ίδια ακριβώς λύση έκανε και μια μαθήτριά μου , της είπα να μου τη στείλει και την έστειλε τελικά σε εικόνα . Την ...κρεμάς μετά ή όχι !!!Ραϊκόφτσαλης Θωμάς έγραψε:Μπάμπη καλησπέρα.
Στο θέμα 3Βγ μια ωραία λύση που έδωσε μαθητής μου είναι η εξής:
Βρήκε το όρια\displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = + \inftyκαι
\displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = - \inftyοπότε ....
Θωμάς
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Μπάμπη, ωραία η πρωτοβουλία για το ανέβασμα πολλών διαφορετικών λύσεων - σκέφτηκε ανάλογα κι ο Ροδόλφος απ' ό,τι βλέπω. Επίσης, επαινετή η ενέργεια του Υπουργείου να δημιουργήσει δίαυλο επικοινωνίας μεταξύ των βαθμολογικών κέντρων, μέτρο που συμβάλλει στην ομογενοποίηση της βαθμολογίας και πρέπει να επεκταθεί του χρόνου. Γιατί φέτος εφαρμόζεται πιλοτικά και μόνο σε 4 μαθήματα στα οποία συμπεριλαμβάνονται τα μαθηματικά γενικής παιδείας όχι όμως και της κατεύθυνσης. Αυτό σημαίνει ότι δεν υπάρχει δυνατότητα επικοινωνίας μεταξύ των βαθμολογικών κέντρων για τα σημερινά θέματα και ό,τι παρουσιαστεί εδώ είναι για ιδία χρήση.
Λεωνίδας
Λεωνίδας
Κάνε το θαύμα για να τ' αρνηθείς (Α. Μπρετόν - Π. Ελυάρ)
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Λεωνίδα, θα το κοιτάξω το απόγευμα. Νομίζω ότι τα Β.Κ. κέντρα μπορούν να επικοινωνούν μεταξύ τους, απλά δεν θα υπάρξει αρμόδιος από την ΚΕΓΕ να απαντήσει στις ερωτήσεις. Οι συντονιστές μπορούν να ανταλλάσσουν ελεύθερα ιδέες .
Δεν αποκλείεται όμως να μην είναι έτσι. Απλά έτυχε να δώ στη σελίδα τη δημιουργία υποενοτήτων για όλα τα μαθήματα. Αν δεν λειτουργήσουν όλα, θα είναι κρίμα, διότι ούτε το Υπουργείο επιβαρύνουμε με έξοδα ούτε κανέναν. Μόνο όφελος μπορεί να υπάρξει από την επικοινωνία των συντονιστών και αυτό χωρίς να κουράσει ΄λη να δεσμεύσει κανέναν από την ΚΕΓΕ!
Θα το εξετάσω όμως και τα ξαναλέμε !
Μπάμπης
Δεν αποκλείεται όμως να μην είναι έτσι. Απλά έτυχε να δώ στη σελίδα τη δημιουργία υποενοτήτων για όλα τα μαθήματα. Αν δεν λειτουργήσουν όλα, θα είναι κρίμα, διότι ούτε το Υπουργείο επιβαρύνουμε με έξοδα ούτε κανέναν. Μόνο όφελος μπορεί να υπάρξει από την επικοινωνία των συντονιστών και αυτό χωρίς να κουράσει ΄λη να δεσμεύσει κανέναν από την ΚΕΓΕ!
Θα το εξετάσω όμως και τα ξαναλέμε !
Μπάμπης
-
Nick Rapanos
- Δημοσιεύσεις: 51
- Εγγραφή: Τρί Απρ 07, 2009 2:18 am
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
sygxoreste me gia ta greeklish alla den exo elliniko pliktrologio.
k. babi thelo na sas rotiso kati gia logariasmo kapoiou filou pou edine.
loipon sto 2Ab vrike tin apostasi d (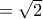 ) tou O apo tin eutheia e me ton tupo tis b lukeiou kai istera epalitheuse oti o migadikos pou dinotan stin ekfonisi exei metro iso me
) tou O apo tin eutheia e me ton tupo tis b lukeiou kai istera epalitheuse oti o migadikos pou dinotan stin ekfonisi exei metro iso me 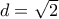 . tora austira tha eprepe na grapsei sto grapto oti einai to simeio epafis tis e me ton kuklo (O,d) alla den to ekane gt theorise dedomeno apo tin ekfonisi oti einai lush tis eutheias (grafei i ekfonisi "apo tous parapano migadikous..." )
. tora austira tha eprepe na grapsei sto grapto oti einai to simeio epafis tis e me ton kuklo (O,d) alla den to ekane gt theorise dedomeno apo tin ekfonisi oti einai lush tis eutheias (grafei i ekfonisi "apo tous parapano migadikous..." )
poia einai i gnomi sas kai pos tha to vathmologousate?
k. babi thelo na sas rotiso kati gia logariasmo kapoiou filou pou edine.
loipon sto 2Ab vrike tin apostasi d (
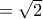 ) tou O apo tin eutheia e me ton tupo tis b lukeiou kai istera epalitheuse oti o migadikos pou dinotan stin ekfonisi exei metro iso me
) tou O apo tin eutheia e me ton tupo tis b lukeiou kai istera epalitheuse oti o migadikos pou dinotan stin ekfonisi exei metro iso me 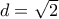 . tora austira tha eprepe na grapsei sto grapto oti einai to simeio epafis tis e me ton kuklo (O,d) alla den to ekane gt theorise dedomeno apo tin ekfonisi oti einai lush tis eutheias (grafei i ekfonisi "apo tous parapano migadikous..." )
. tora austira tha eprepe na grapsei sto grapto oti einai to simeio epafis tis e me ton kuklo (O,d) alla den to ekane gt theorise dedomeno apo tin ekfonisi oti einai lush tis eutheias (grafei i ekfonisi "apo tous parapano migadikous..." )poia einai i gnomi sas kai pos tha to vathmologousate?
- nsmavrogiannis
- Επιμελητής
- Δημοσιεύσεις: 4479
- Εγγραφή: Σάβ Δεκ 20, 2008 7:13 pm
- Τοποθεσία: Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Aν και η ερώτηση απευθύνεται στον Μπάμπη Στεργίου ενημερώτικά θα ήθελα να πώ ότι η παραπάνω αντιμετώπιση δεν στερείται αυστηρότητας και δεν θα έπρεπε να προστεθεί τίποτα άλλο. Η απάντηση θεωρείται σωστή. Στο δικό μας βαθμολογικό κέντρο, αν και φαντάζομαι και στα άλλα, παίρνει το σύνολο των μονάδων.Nick Rapanos έγραψε: tora austira tha eprepe
Μαυρογιάννης
Αν κανείς δεν ελπίζει, δεν θα βρεί το ανέλπιστο, οι δρόμοι για το ανεξερεύνητο θα είναι κλειστοί.
Ηράκλειτος
Ηράκλειτος
-
Nick Rapanos
- Δημοσιεύσεις: 51
- Εγγραφή: Τρί Απρ 07, 2009 2:18 am
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
k. mavrogianni sas efxaristo polu gia tin apantisi. elpizo mono na min uparksei provlhma se alla eksetastika kentra kai na mhn einai sto xeri tou kathe vathmologiti na kopsei monades kata tin krisi tou.nsmavrogiannis έγραψε:Aν και η ερώτηση απευθύνεται στον Μπάμπη Στεργίου ενημερώτικά θα ήθελα να πώ ότι η παραπάνω αντιμετώπιση δεν στερείται αυστηρότητας και δεν θα έπρεπε να προστεθεί τίποτα άλλο. Η απάντηση θεωρείται σωστή. Στο δικό μας βαθμολογικό κέντρο, αν και φαντάζομαι και στα άλλα, παίρνει το σύνολο των μονάδων.Nick Rapanos έγραψε: tora austira tha eprepe
Μαυρογιάννης
tora pou to ksanavlepo to thema exete apoluto dikio oti den stereitai austirotitas otan i ekfonisi mas epitrepei na theorisoume oti o 1-i einai apo to sugekrimeno sunolo ton migadikon.
ps. exete kanei exairetiki douleia me tin istoselida sas. bravo sas!
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Καλημέρα σε όλους.
Στο συνημένο αρχείο θα δείτε λύσεις και τον τρόπο βαθμολόγησης σε κάποιο βαθμολογικό κέντρο.
Θωμάς
Υ.Γ
Μετέτρεψα το αρχείο σε word 2003 για να διαβάζετε από όλους
Στο συνημένο αρχείο θα δείτε λύσεις και τον τρόπο βαθμολόγησης σε κάποιο βαθμολογικό κέντρο.
Θωμάς
Υ.Γ
Μετέτρεψα το αρχείο σε word 2003 για να διαβάζετε από όλους
- Συνημμένα
-
- endeiktikes_bathmologies.doc
- (4.23 MiB) Μεταφορτώθηκε 497 φορές
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
- ΧΡΗΣΤΟΣ ΚΑΡΔΑΣΗΣ
- Δημοσιεύσεις: 704
- Εγγραφή: Κυρ Μάιος 17, 2009 7:07 pm
- Τοποθεσία: ΚΑΒΑΛΑ
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Νίκο , καλημέρα !Nick Rapanos έγραψε:sygxoreste me gia ta greeklish alla den exo elliniko pliktrologio.
k. babi thelo na sas rotiso kati gia logariasmo kapoiou filou pou edine.
loipon sto 2Ab vrike tin apostasi d () tou O apo tin eutheia e me ton tupo tis b lukeiou kai istera epalitheuse oti o migadikos pou dinotan stin ekfonisi exei metro iso me
. tora austira tha eprepe na grapsei sto grapto oti einai to simeio epafis tis e me ton kuklo (O,d) alla den to ekane gt theorise dedomeno apo tin ekfonisi oti einai lush tis eutheias (grafei i ekfonisi "apo tous parapano migadikous..." )
poia einai i gnomi sas kai pos tha to vathmologousate?
Εμείς δεν θα κόψουμε τίποτα(δεν βλέπω τον λόγο !). Αλλά μου φάνηκε ότι χθες άκουσα έναν συνάδελφο ότι τους είπαν να αφαιρέσουν κάτι , αν δεν αναφέρουν μια προτασούλα που δεν θυμάμαι και που εκείνη τη στιγμή δεν μπόσεσα τηλεφωνικά να την αξιολογήσω! Θα επικοινωνήσω πάλι μαζί του , να δω τι αποφάσισαν !
Ό,τι όμως και να είναι , η βαθμολογία θα είναι σχεδόν πλήρης !
Εξ 'άλλου , σε πολλές περιπτώσεις, οι βαθμολογητές όταν είναι για μια μονάδα , δεν ευθυγραμμίζονται με την γενική μοριοδότηση, ειδικά όταν είναι σίγουροι ότι έχουν δίκαιο και δεν κόβουν ούτε αυτή τη μονάδα!
Καλή σου μέρα !
Μπάμπης
-
polydeykhs
- Δημοσιεύσεις: 13
- Εγγραφή: Τρί Δεκ 30, 2008 7:05 pm
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Τελικά δεν απαντήθηκε αν φθάνει μόνο η εύρεση των δυο άπειρων ορίων χωρίς επίκληση της μονοτονίας για τον ισχυρισμό ότι το σύνολο τιμών είναι το R.Ραϊκόφτσαλης Θωμάς έγραψε:Μπάμπη καλησπέρα.
Στο θέμα 3Βγ μια ωραία λύση που έδωσε μαθητής μου είναι η εξής:
Βρήκε το όρια\displaystyle \mathop {\ell im}\limits_{x \to {1^ + }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = + \inftyκαι
\displaystyle \mathop {\ell im}\limits_{x \to {2^ - }} \frac{{f(\beta ) - 1}}
{{x - 1}} + \frac{{f(\gamma ) - 1}}
{{x - 2}} = - \inftyοπότε ....
Θωμάς
Υπάρχουν κάποιοι παιδαγωγικοί λόγοι;
Γνώμη μου είναι ότι χωρίς τη μονοτονία είναι ελλιπής ο ισχυρισμός αλλά βέβαια όχι όλο λάθος.
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Συνάδελφε Αποστόλη Παπανικολάου,
να ζητήσω συγνώμη για την παράλειψή μου.
Επειδή η συνάρτηση είναι συνεχής στο (1,2) και γνωρίζοντας ότι το σύνολο τιμών μιας συνεχούς συνάρτησης ορισμένη σε διάστημα είναι διάστημα, συμπεραίνουμε τελικά ότι η συνάρτηση έχει σύνολο τιμών το R.
Στη συνέχεια επειδή το 0 (μηδέν) ανήκει στο σύνολο τιμών συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα Xo ώστε f(Xo)=0
Ελπίζω να σε κάλυψα.
Θωμάς
να ζητήσω συγνώμη για την παράλειψή μου.
Επειδή η συνάρτηση είναι συνεχής στο (1,2) και γνωρίζοντας ότι το σύνολο τιμών μιας συνεχούς συνάρτησης ορισμένη σε διάστημα είναι διάστημα, συμπεραίνουμε τελικά ότι η συνάρτηση έχει σύνολο τιμών το R.
Στη συνέχεια επειδή το 0 (μηδέν) ανήκει στο σύνολο τιμών συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα Xo ώστε f(Xo)=0
Ελπίζω να σε κάλυψα.
Θωμάς
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Για το 4 α)
Σύμφωνα με τη διατύπωση , θεωρούμε δεδομένο ότι όλες οι εικόνες βρισκονται σε ευθεία της οποίας απλά αναζητούμε την εξίσωση.
Οπότε αν ενας μαθητής πάρει δυο συγκεκριμένους μιγαδικούς (πχ για λ=0 και λ=1) και βρει την ευθεία y=x-2 πανω στην οποία βρίσκονται τότε είναι οκ.
Γιατί εφόσον δεχόμαστε ότι όλοι βρίσκονται πάνω σε ευθεία και δύο από αυτούς ανήκουν σ'αυτή τότε ολοι θα βρίσκονται σε αυτή
Για το 4 γ)
έστω για κάθε
για κάθε  , τότε ως συνεχής διατηρεί πρόσημο. Η G΄(x) επίσης σταθερό πρόσημο. Άρα G γνησίως μονότονη στο [0,2] (συνεχής). Οπότε G(0)<G(2) ή G(0)>G(2) Δηλαδή 3<3 ή 3>3.
, τότε ως συνεχής διατηρεί πρόσημο. Η G΄(x) επίσης σταθερό πρόσημο. Άρα G γνησίως μονότονη στο [0,2] (συνεχής). Οπότε G(0)<G(2) ή G(0)>G(2) Δηλαδή 3<3 ή 3>3.
ή G 1-1, άρα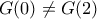
Σε κάθε περίπτωση άτοπο
Σύμφωνα με τη διατύπωση , θεωρούμε δεδομένο ότι όλες οι εικόνες βρισκονται σε ευθεία της οποίας απλά αναζητούμε την εξίσωση.
Οπότε αν ενας μαθητής πάρει δυο συγκεκριμένους μιγαδικούς (πχ για λ=0 και λ=1) και βρει την ευθεία y=x-2 πανω στην οποία βρίσκονται τότε είναι οκ.
Γιατί εφόσον δεχόμαστε ότι όλοι βρίσκονται πάνω σε ευθεία και δύο από αυτούς ανήκουν σ'αυτή τότε ολοι θα βρίσκονται σε αυτή
Για το 4 γ)
έστω
 για κάθε
για κάθε  , τότε ως συνεχής διατηρεί πρόσημο. Η G΄(x) επίσης σταθερό πρόσημο. Άρα G γνησίως μονότονη στο [0,2] (συνεχής). Οπότε G(0)<G(2) ή G(0)>G(2) Δηλαδή 3<3 ή 3>3.
, τότε ως συνεχής διατηρεί πρόσημο. Η G΄(x) επίσης σταθερό πρόσημο. Άρα G γνησίως μονότονη στο [0,2] (συνεχής). Οπότε G(0)<G(2) ή G(0)>G(2) Δηλαδή 3<3 ή 3>3.ή G 1-1, άρα
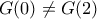
Σε κάθε περίπτωση άτοπο
Δεν μπορεί κάποιος να αποκτήσει γνώση αν πιστεύει ότι την έχει.
-
polydeykhs
- Δημοσιεύσεις: 13
- Εγγραφή: Τρί Δεκ 30, 2008 7:05 pm
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Διάστημα ναι αλλά όχι κατ ανάγκην το διάστημα με άκρα τα όρια στα άκρα του διαστήματος ορισμού αν δεν είναι γνησίως μονότονη η συνάρτηση.Ραϊκόφτσαλης Θωμάς έγραψε:Συνάδελφε Αποστόλη Παπανικολάου,
να ζητήσω συγνώμη για την παράλειψή μου.
Επειδή η συνάρτηση είναι συνεχής στο (1,2) και γνωρίζοντας ότι το σύνολο τιμών μιας συνεχούς συνάρτησης ορισμένη σε διάστημα είναι διάστημα, συμπεραίνουμε τελικά ότι η συνάρτηση έχει σύνολο τιμών το R.
Στη συνέχεια επειδή το 0 (μηδέν) ανήκει στο σύνολο τιμών συμπεραίνουμε ότι υπάρχει τουλάχιστον ένα Xo ώστε f(Xo)=0
Ελπίζω να σε κάλυψα.
Θωμάς
Αν πρόσεξες είπα να βρει κανείς τα δυο άπειρα όρια και να συμπεράνει σύνολο τιμών R χωρίς να επικαλεστεί τη μονοτονία.Εκεί τοποθετείται το ερώτημα.
Θα μου πεις αφού είναι τα δυο άπειρα δηλαδή το μέγιστο διάστημα τι άλλο θα μπορούσε να συμβεί;
Κάπου δε μου κάθεται, εννοώ ότι νομίζω ότι θέλει απόδειξη αν δεν επικαλεστείς μονοτονία.
Ευχαριστώ
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
kapapi έγραψε:Για το 4 α)
Σύμφωνα με τη διατύπωση , θεωρούμε δεδομένο ότι όλες οι εικόνες βρισκονται σε ευθεία της οποίας απλά αναζητούμε την εξίσωση.
Οπότε αν ενας μαθητής πάρει δυο συγκεκριμένους μιγαδικούς (πχ για λ=0 και λ=1) και βρει την ευθεία y=x-2 πανω στην οποία βρίσκονται τότε είναι οκ.
Γιατί εφόσον δεχόμαστε ότι όλοι βρίσκονται πάνω σε ευθεία και δύο από αυτούς ανήκουν σ'αυτή τότε ολοι θα βρίσκονται σε αυτή
Είναι γεγονός ότι η διατύπωση επιβάλει να θεωρήσουμε πλήρως αποδεκτή και αυτή τη λύση. Θάταν βέβαια πολύ πιο εύστοχο το ερώτημα να δοθεί κάπως έτσι :
'' δείξτε ότι οι εικόνες των μιγαδικών... βρίσκονται σε μια ευθεία(γραμμή) και να βρείτε την εξίσωσή της ''.
Ίσως το απέφυγαν διότι το ''δείξτε'' και το '' βρείτε '' εδώ συμπίπτουν. Τέλος πάντων, δεν νομίζω ότι θα χάσει κάποιος άσκοπα μόρια, αλλά αν αρχίσει η διόρθωση θα ξέρουμε από πρώτο χέρι τι ακριβώς γράφουν τα παιδιά !
Καλό μεσημέρι !
Μπάμπης
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Αποστόλη,
γενικά το σύνολο τιμών δεν είναι κατ΄ανάγκη το διάστημα που καθορίζουν οι οριακές τιμές στα άκρα, αλλά όταν αυτά είναι αντίστοιχα το -οο και το +00 τότε είναι προφανές ότι το σύνολο τιμών είναι το R.
Θωμάς
γενικά το σύνολο τιμών δεν είναι κατ΄ανάγκη το διάστημα που καθορίζουν οι οριακές τιμές στα άκρα, αλλά όταν αυτά είναι αντίστοιχα το -οο και το +00 τότε είναι προφανές ότι το σύνολο τιμών είναι το R.
Θωμάς
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
-
polydeykhs
- Δημοσιεύσεις: 13
- Εγγραφή: Τρί Δεκ 30, 2008 7:05 pm
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Η διαφωνία μας είναι στο "προφανώς".Ραϊκόφτσαλης Θωμάς έγραψε:Αποστόλη,
γενικά το σύνολο τιμών δεν είναι κατ΄ανάγκη το διάστημα που καθορίζουν οι οριακές τιμές στα άκρα, αλλά όταν αυτά είναι αντίστοιχα το -οο και το +00 τότε είναι προφανές ότι το σύνολο τιμών είναι το R.
Θωμάς
- Ραϊκόφτσαλης Θωμάς
- Δημοσιεύσεις: 1112
- Εγγραφή: Κυρ Δεκ 21, 2008 12:01 am
- Τοποθεσία: Άλιμος, Αθήνα
- Επικοινωνία:
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Άσε να υπάρχει και μια διαφωνία, η οποία μόνο καλό μας κάνειpolydeykhs έγραψε:Η διαφωνία μας είναι στο "προφανώς".Ραϊκόφτσαλης Θωμάς έγραψε:Αποστόλη,
γενικά το σύνολο τιμών δεν είναι κατ΄ανάγκη το διάστημα που καθορίζουν οι οριακές τιμές στα άκρα, αλλά όταν αυτά είναι αντίστοιχα το -οο και το +00 τότε είναι προφανές ότι το σύνολο τιμών είναι το R.
Θωμάς
Με εκτίμηση
Θωμάς
Η γνώση μας κάνει περήφανους, η σοφία ταπεινούς.
-
Μπάμπης Στεργίου
- Επιμελητής
- Δημοσιεύσεις: 5577
- Εγγραφή: Δευ Δεκ 22, 2008 2:16 pm
- Τοποθεσία: Χαλκίδα - Καρδίτσα
Re: ΔΙΑΦΟΡΕΤΙΚΕΣ ΛΥΣΕΙΣ - ΕΞΕΤΑΣΕΙΣ 2009
Δεν έχω τον απαιτούμενο χρόνο, αλλά θα προσπαθήσω να βοηθήσω με δυο λόγια:polydeykhs έγραψε:
Διάστημα ναι αλλά όχι κατ ανάγκην το διάστημα με άκρα τα όρια στα άκρα του διαστήματος ορισμού αν δεν είναι γνησίως μονότονη η συνάρτηση.
Αν πρόσεξες είπα να βρει κανείς τα δυο άπειρα όρια και να συμπεράνει σύνολο τιμών R χωρίς να επικαλεστεί τη μονοτονία.Εκεί τοποθετείται το ερώτημα.
............................Κάπου δε μου κάθεται, εννοώ ότι νομίζω ότι θέλει απόδειξη αν δεν επικαλεστείς μονοτονία.
Ευχαριστώ
α) Η συνέχεια πχ στο διάστημα Δ = (1,2) είναι δεδομένη .
β) Τα όρια στα άκρα του Δ είναι άπειρα (με αντίθετο πρόσημο)
γ) Η εικόνα του διαστήματος Δ είναι διάστημα.
Μπορεί τώρα τα άκρα αυτού του διαστήματος f(Δ) να μην είναι άπειρα ; Όχι, διότι τότε το f(Δ) θα ήταν φραγμένο τουλάχστον από τη μία μεριά, άτοπο !
Μπορείς όμως και με άλλους παρόμοιους συλλογισμούς να καταλήξεις στο ίδιο συμπέρασμα.
ΣΧΟΛΙΟ
Η μονοτονία στο σχετικό θεώρημα του βιβλίου χρειάζεται μόνο για να εξασφαλιστεί ότι δεν θα υπάρξουν τιμές της f έξω από το διάστημα των ορίων Α, Β.Για κανένα άλλο λόγο. Προσπάθησε να αποδείξεις το θεώρημα αυτό(έχει λεπτή απόδειξη) και θα καταλάβεις πιο καλά γιατί στην περίπτωσή μας η μονοτονία δε χρειάζεται.
Στην πραγματικότητα αυτό το συμπέρασμα θα έπρεπε να το γράφει το σχολικό ως απλή παρατήρηση κάτω από την εν λόγω πρόταση.Το έχω όμως γράψει σε βιβλίο και ο ίδιος .
Το θέμα το έχουμε ξανακουβεντιάσει στο mathematica και έχουμε κάνει την απόδειξη( Είχα θέσει ο ίδιος το ερώτημα και νομίζω ότι είχαν γράψει τις σκέψεις τους , μεταξύ άλλων , ο Νίκος Μαυρογιάννης και ο Κώστας Σερίφης ).
Μπάμπης
Μέλη σε σύνδεση
Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης
