Αν
 διαιρεί τον αριθμό
διαιρεί τον αριθμό  ,
,  φυσικός, τότε
φυσικός, τότε  ;
;(Θαλής Γ!γυμν. 1994)
Συντονιστές: cretanman, Demetres, polysot, socrates, silouan
 διαιρεί τον αριθμό
διαιρεί τον αριθμό  ,
,  φυσικός, τότε
φυσικός, τότε  ;
;Ας ονομάσουμε χ την μεγάλη βάση και y την μικρή του ισοσκελούς τραπεζίου. Από την υπόθεση, έχουμε ότιΔΗΜΗΤΡΗΣ έγραψε:
ΑΣΚΗΣΗ 158:
Οι μη παράλληλες πλευρές ισοσκελούς τραπεζίου έχουν μήκη 10 m η κάθε μία, ενώ η περίμετρός του είναι 152 m. Αν το ύψος του είναι το 1/9 της μεγάλης βάσης και οι βάσεις του είναι ανάλογες προς τους αριθμούς 6 και 5, να υπολογίσετε το εμβαδόν του.








Έχουμε:S.E.Louridas έγραψε:ΑΣΚΗΣΗ 164 :
Επιλύσατε στους θετικούς ακέραιους την εξίσωση που ακολουθεί:



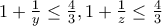

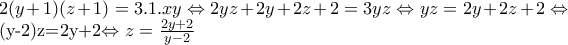 (αφού προφανώς είναι
(αφού προφανώς είναι 


Ας υποθέσουμε ότι:S.E.Louridas έγραψε:ΑΣΚΗΣΗ 164 :
Επιλύσατε στους θετικούς ακέραιους την εξίσωση που ακολουθεί:

 άτοπο.
άτοπο.

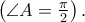
 υπολογίστε το εμβαδό του τριγώνου ABC.
υπολογίστε το εμβαδό του τριγώνου ABC.S.E.Louridas έγραψε:ΑΣΚΗΣΗ 164
Επιλύσατε στους θετικούς ακέραιους την εξίσωση που ακολουθεί:
S.E.Louridas
 που ικανοποιούν την εξίσωση
που ικανοποιούν την εξίσωση 
 ισχύει ότι
ισχύει ότι 

 είναι τέτοιοι ώστε
είναι τέτοιοι ώστε 

 είναι τέτοιοι ώστε
είναι τέτοιοι ώστε 
 ένα σύνολο ακεραίων, τέτοιο ώστε
ένα σύνολο ακεραίων, τέτοιο ώστε
 τέτοιοι ώστε
τέτοιοι ώστε 

Ας υποθέσουμε ότι ο βοηθός θα πάρει x ευρώ. Τότε ο επιστήμονας θα πάρειΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 160 :
Ένας επιστήμονας και ο βοηθός του ανέλαβαν μια έρευνα σε χημικό εργαστήριο από την οποία θα εισπράξουν 85116 ευρώ. Ο επιστήμονας θα απασχοληθεί για 42 μέρες και ο βοηθός του για 45 μέρες. Η ημερήσια αμοιβή του επιστήμονα είναι κατά 40% μεγαλύτερη της ημερήσιας αμοιβής του βοηθού του. Πόσα χρήματα θα εισπράξει ο καθένας στο τέλος της έρευνας;
 ευρώ
ευρώ
Ο αριθμός που προκύπτει είναι ο 19901991199219931994199519961997ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 165 :
Γράφουμε στη σειρά τους αριθμούς από το 1990 έως και το 1997. Να εξετάσετε αν ο αριθμός που προκύπτει είναι πρώτος.
(α) Η γωνία ΑΔΓ είναι εγγεγραμμένη και βαίνει σε ημικύκλιο. Άρα είναι ορθή και άρα το ΑΔ είναι ύψος του ισοσκελούς τριγώνου ΑΒΓ.ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 166 :
Δίνεται ισοσκελές τρίγωνο ΑΒΓ (ΑΒ=ΑΓ). Με διάμετρο την πλευρά ΑΓ γράφουμε κύκλο που τέμνει την πλευρά ΒΓ στο Δ. Φέρνουμε ακόμα την Αχ κάθετη στην ΑΔ που τέμνει τον κύκλο στο Ε.
(1) Να αποδείξετε ότι το ΑΔ είναι ύψος του τριγώνου ΑΒΓ
(2) Να συγκρίνετε το εμβαδόν του τριγώνου ΑΒΓ προς το εμβαδόν του τετραπλεύρου ΑΔΓΕ
socrates έγραψε:
ΑΣΚΗΣΗ 178 :
Έστωένα σύνολο ακεραίων, τέτοιο ώστε
Να δείξετε ότι:
α) υπάρχουν μη μηδενικοί και διαφορετικοί ανά δύοτέτοιοι ώστε
β)
 είναι στοιχεία τού
είναι στοιχεία τού  .
. . Έχουμε
. Έχουμε 

 παίρνουμε ότι
παίρνουμε ότι 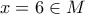 επομένως θα ισχύει καί
επομένως θα ισχύει καί  .
. παίρνουμε πως
παίρνουμε πως  .
. βρίσκουμε ότι
βρίσκουμε ότι  .
. , το ζητούμενο έπεται.
, το ζητούμενο έπεται. αρκεί να δείξουμε οτί
αρκεί να δείξουμε οτί  . Όμως, συμφωνα με τον τελευταίο κανόνα για να δείξουμε οτί
. Όμως, συμφωνα με τον τελευταίο κανόνα για να δείξουμε οτί  αρκεί να είναι:
αρκεί να είναι: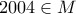 . Αλλά για να δείξουμε οτί
. Αλλά για να δείξουμε οτί 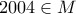
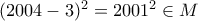 δηλαδή οτί
δηλαδή οτί  . Eπαναλαμβάνωντας συνεχώς τα βήματα αυτα αρκεί να είναι
. Eπαναλαμβάνωντας συνεχώς τα βήματα αυτα αρκεί να είναι  . Το οποίο ισχύει, αφού
. Το οποίο ισχύει, αφού  καί 2001=πολ.3
καί 2001=πολ.3Έχω ότι :ΔΗΜΗΤΡΗΣ έγραψε:ΑΣΚΗΣΗ 168 :
Δίνεται τρίγωνο ΑΒΓ με πλευρές ΑΒ=6, ΒΓ=8 και έστω ΑΜ διάμεσος αυτού. Η μεσοκάθετη της διαμέσου ΑΜ τέμνει την πλευρά ΑΓ στο σημείο Ε. Αν οι πλευρές ΑΒ,ΑΓ και ΒΓ είναι ανάλογες προς τις πλευρές ΕΜ, ΜΓ και ΕΓ του τριγών ου ΕΜΓ αντίστοιχα, να βρεθεί το μήκος της πλευράς ΑΓ.

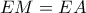






Έστω ότι ο ψαράς είχε ψαρέψειΦερμά_96 έγραψε:
ΑΣΚΗΣΗ 170 :
ένας ερασιτέχνης ψαράς, αποφασίζει μια μέρα, με ευκαιρεία το ψάρεμα του να κάνει κάποιες επισκέψης στους φίλους του. Ξεκινάει λοιπόν από την θάλασσα όπου και ψάρευε, πέρνει μαζί του τα ψάρια που ψάρεψε στην θάλασσα, και πάει να βρει τους φίλους του. Οι φίλοι του είναι. μένουν σε
διαφορετικά σπίτια, και πριν πάει σε κάθε σπίτι πρέπει να περάσει από ένα ποτάμι. Σε κάθε ποτάμι ψαρεύει, και διπλασιάζει τα ψάρια που έχει εκείνη την στιγμή. Ξεκινάει λοιπόν για το πρώτο σπίτι, και περνάει από το πρώτο ποτάμι όπου ψαρεύει. Φτάνει στον φίλο του, στον οποίο και δείνει λίγα ψάρια. Φεύγει, και περνάει από ένα δεύτερο ποτάμι, ψαρεύει, και καταλήγει στον δεύτερο φίλο του, στον οποίο δείνει μια ποσότητα ψαριών, ίση με αυτή που έδωσε στον προηγούμενο. Τέλος, περνάει από το τρίτο ποτάμι, ψαρεύει, και δείνει στον τρίτο φίλο του μια ποσότητα ψαριών ίση με αυτή που ήδη έδωσε στον καθένα από τους δυο προηγούμενος. Αν του περίσσεψε ακριβώς ένα ψάρι, να βρείτε πόσα ψάρια μπορεί να είχε στην αρχή.(όλες τις πιθανές τιμές)
 ψάρια στην θάλασσα και ότι σε κάθε σπίτι, άφηνε από
ψάρια στην θάλασσα και ότι σε κάθε σπίτι, άφηνε από 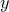 ψάρια.
ψάρια. ,αφήνει
,αφήνει  ψάρια στο πρώτο σπίτι και άρα του μένουν
ψάρια στο πρώτο σπίτι και άρα του μένουν  ψάρια.
ψάρια. , αφήνει
, αφήνει  ψάρια στο δεύτερο σπίτι και άρα του μένουν
ψάρια στο δεύτερο σπίτι και άρα του μένουν  ψάρια.
ψάρια. , αφήνει
, αφήνει  ψάρια στο τρίτο σπίτικαι άρα του μένουν
ψάρια στο τρίτο σπίτικαι άρα του μένουν  ψάρια.
ψάρια.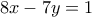



 να είναι αρνητικός ακέραιος (αφού οι αριθμοί
να είναι αρνητικός ακέραιος (αφού οι αριθμοί  και
και πρέπει να είναι θετικοί ακέραιοι)
πρέπει να είναι θετικοί ακέραιοι)Τα τρίγωναS.E.Louridas έγραψε:ΑΣΚΗΣΗ 174 :
Έστω ορθογώνιο τρίγωνο
Αν ο εγγεγραμμένος κύκλος στο τρίγωνο, εφάπτεται στην υποτείνουσα
στο σημείο
και δίνονται τα μήκη
υπολογίστε το εμβαδό του τριγώνου
.
 και
και  επειδή είναι ορθογώνια ,είναι ίσα ως πλευρα-γωνια. Άρα η πλευρά
επειδή είναι ορθογώνια ,είναι ίσα ως πλευρα-γωνια. Άρα η πλευρά  είναι ίση με το
είναι ίση με το  .
. και
και  και η πλευρά
και η πλευρά  είναι ίση με το
είναι ίση με το  .
. επειδή τα τρίγωνα
επειδή τα τρίγωνα  ,
,  είναι ορθογώνια και έχουν τη μια τους γωνία
είναι ορθογώνια και έχουν τη μια τους γωνία 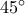 ,είναι και ισοσκελή άρα
,είναι και ισοσκελή άρα  .
.


 παίρνω μόνο τη θετική ρίζα
παίρνω μόνο τη θετική ρίζα

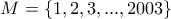 . Πόσα υποσύνολα του Μ υπάρχουν με άρτιο πλήθος στοιχείων;
. Πόσα υποσύνολα του Μ υπάρχουν με άρτιο πλήθος στοιχείων;Ας μου επιτραπεί να συγχαρώ την μικρή αλλά μεγάλη σε Μαθηματικό ταλέντο Γιώτα και γιά την λύση της στην Άσκηση 174.S.E.Louridas έγραψε:ΑΣΚΗΣΗ 174 :
Έστω ορθογώνιο τρίγωνο
Αν ο εγγεγραμμένος κύκλος στο τρίγωνο, εφάπτεται στην υποτείνουσα
στο σημείο
και δίνονται τα μήκη
υπολογίστε το εμβαδό του τριγώνου
.

 όταν
όταν 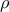 είναι η ακτίνα του εγγεγραμμένου κύκλου.
είναι η ακτίνα του εγγεγραμμένου κύκλου.Ανspiros filippas έγραψε: ΑΣΚΗΣΗ 179 :
Θεωρούμε το σύνολο. Πόσα υποσύνολα του Μ υπάρχουν με άρτιο πλήθος στοιχείων;
 ένα υποσύνολο του
ένα υποσύνολο του  με άρτιο πλήθος στοιχείων, τότε το συμπλήρωμά του
με άρτιο πλήθος στοιχείων, τότε το συμπλήρωμά του  έχει περιττό, και αντίστροφα. Έτσι ζευγαρώνουμε ένα προς ένα τα υποσύνολα με άρτιο πλήθος με εκείνα που έχουν περιττό. Συνεπώς τα άρτιου πλήθους υποσύνολα είναι ακριβώς τα μισά, δηλαδή
έχει περιττό, και αντίστροφα. Έτσι ζευγαρώνουμε ένα προς ένα τα υποσύνολα με άρτιο πλήθος με εκείνα που έχουν περιττό. Συνεπώς τα άρτιου πλήθους υποσύνολα είναι ακριβώς τα μισά, δηλαδή  .
.  σύνολα)
σύνολα)(*) Με την παράκληση εμείς οι μεγάλοι έφηβοι να αφήσουμε 1-2 μέρες τους μικρούς έφηβους, αλλά που αγαπούν τα Μαθηματικά μας, να ασχοληθούν.Demetres έγραψε: ...Μια στρατηγική επίλυσης προβλημάτων συνοψίζεται στο εξής: «Αν δεν μπορείς να λύσεις ένα πρόβλημα, τότε βρες και λύσε ένα πιο εύκολο πρόβλημα το οποίο σχετίζεται με το αρχικό.
Έχουμε:Karanus έγραψε:ΑΣΚΗΣΗ 172 :
Ανδιαιρεί τον αριθμό
,
φυσικός, τότε

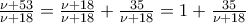
 να είναι διαιρέτης του 35. Και δεδομένου ότι ο αριθμός
να είναι διαιρέτης του 35. Και δεδομένου ότι ο αριθμός  είναι θετικός, θα πρέπει:
είναι θετικός, θα πρέπει: , πράγμα άτοπο, αφου
, πράγμα άτοπο, αφου  ή
ή , ομοίως άτοπο ή
, ομοίως άτοπο ή  , ομοίως άτοπο ή
, ομοίως άτοπο ή  από όπου προκύπτει
από όπου προκύπτει 
Από την υπόθεση, έχουμε ότιsocrates έγραψε:Άσκηση 175
Αν για τους πραγματικούς αριθμούςισχύει ότι

να δείξετε ότι
Ισχύει το αντίστροφο;
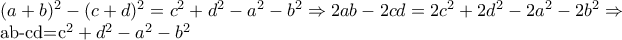
 (1)
(1)![(a+b)^{4}-(c+d)^{4}= [(a+b)^{2}-(c+d)^{2}][(a+b)^{2}+(c+d)^{2}]= (a+b)^{4}-(c+d)^{4}= [(a+b)^{2}-(c+d)^{2}][(a+b)^{2}+(c+d)^{2}]=](/forum/ext/geomar/texintegr/latexrender/pictures/050540240a71d8ef2be81fe2d6f23df1.png)
![(ab-cd)[a^{2}+b^{2}+c^{2}+d^{2}+2(ab+cd)]= (ab-cd)[a^{2}+b^{2}+c^{2}+d^{2}+2(ab+cd)]=](/forum/ext/geomar/texintegr/latexrender/pictures/4d239add522e30203cc3391e45caa064.png)


![[(c^{2}+d^{2})-(a^{2}+b^{2})][(c^{2}+d^{2})+(a^{2}+b^{2})]+2a^{2}b^{2}-2c^{2}d^{2}= [(c^{2}+d^{2})-(a^{2}+b^{2})][(c^{2}+d^{2})+(a^{2}+b^{2})]+2a^{2}b^{2}-2c^{2}d^{2}=](/forum/ext/geomar/texintegr/latexrender/pictures/3854c971aa62a481548b6f85f4a9f94d.png)




Με ύψωση στο τετράγωνο, έχουμε:socrates έγραψε:Άσκηση 176
Αν οι πραγματικοί αριθμοίείναι τέτοιοι ώστε

να δείξετε ότι

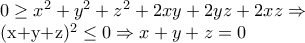
socrates έγραψε: Άσκηση 177
Αν οι πραγματικοί αριθμοίείναι τέτοιοι ώστε

να δείξετε ότι ένας από αυτούς ισούται με το άθροισμα των άλλων δύο.
 τότε ένας από τους
τότε ένας από τους  θα ισούται με το άθροισμα των δύο άλλων)
θα ισούται με το άθροισμα των δύο άλλων) τότε θα έχουμε από τις υποθέσεις ότι:
τότε θα έχουμε από τις υποθέσεις ότι:

 από όπου προκύπτει ότι
από όπου προκύπτει ότι  δηλ.
δηλ. 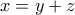 ή
ή
 τότε έχουμε το ζητούμενο.
τότε έχουμε το ζητούμενο.
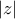 παίρνουμε από τις υποθέσεις:
παίρνουμε από τις υποθέσεις:

![\left|1-\frac{x}{z} \right|\geq \left|\frac{y}{z} \right|] \left|1-\frac{x}{z} \right|\geq \left|\frac{y}{z} \right|]](/forum/ext/geomar/texintegr/latexrender/pictures/d152584f834c40989519d51bb0adc544.png)

 (1)
(1) (2)
(2) (3)
(3) (όμοια θα εργασθούμε και αν
(όμοια θα εργασθούμε και αν  (ενώ η περίπτωση
(ενώ η περίπτωση  προφανώς απορρίπτεται
προφανώς απορρίπτεται

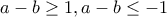 που μας οδηγούν σε άτοπο και άρα η 1η Περίπτωση απορρίπτεται.
που μας οδηγούν σε άτοπο και άρα η 1η Περίπτωση απορρίπτεται.

 . Οπότε οι σχέσεις (1),(2),(3) γράφονται:
. Οπότε οι σχέσεις (1),(2),(3) γράφονται:

 και άρα το ζητούμενο.
και άρα το ζητούμενο.




 , δηλαδή πάλι το ζητούμενο.
, δηλαδή πάλι το ζητούμενο.Υψώνοντας στο τετράγωνο έχουμε:socrates έγραψε: Άσκηση 177
Αν οι πραγματικοί αριθμοίείναι τέτοιοι ώστε

να δείξετε ότι ένας από αυτούς ισούται με το άθροισμα των άλλων δύο.

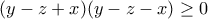



 αν ισχύει
αν ισχύει 
![ab=300+7[a,b]+5(a,b), ab=300+7[a,b]+5(a,b),](/forum/ext/geomar/texintegr/latexrender/pictures/708d1160d615c719bc863c64ef1ac043.png)
![[x,y] [x,y]](/forum/ext/geomar/texintegr/latexrender/pictures/8ca042e8ff30aba99a78e069db08b58a.png) και
και  το ελάχιστο κοινό πολλαπλάσιο και ο μέγιστος κοινός διαιρέτης των
το ελάχιστο κοινό πολλαπλάσιο και ο μέγιστος κοινός διαιρέτης των  αντίστοιχα.
αντίστοιχα. ορθογώνιο στο
ορθογώνιο στο  και έστω
και έστω  το ύψος από την κορυφή
το ύψος από την κορυφή 
 και
και  τέμνουν την πλευρά
τέμνουν την πλευρά  στα σημεία
στα σημεία  και
και  αντίστοιχα.
αντίστοιχα. μονάδες και το μήκος του τμήματος
μονάδες και το μήκος του τμήματος 
 μονάδες,
μονάδες, 
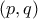 πρώτων αριθμών τέτοια ώστε
πρώτων αριθμών τέτοια ώστε 



socrates έγραψε: Άσκηση 184
Δείξτε ότι
για όλους τους θετικούς πραγματικούς αριθμούς

 άρα μένει να δείξουμε ότι
άρα μένει να δείξουμε ότι
Μια διαφορετική λύση. Αρκεί να δείξουμε ότιsocrates έγραψε: Άσκηση 184
Δείξτε ότι
για όλους τους θετικούς πραγματικούς αριθμούς
 για κάθε θετικούς πραγματικούς
για κάθε θετικούς πραγματικούς  . [Πράγματι, τότε θα έχουμε
. [Πράγματι, τότε θα έχουμε  ]
] ή ισοδύναμα ότι
ή ισοδύναμα ότι  το οποίο ισχύει.
το οποίο ισχύει.Μέλη σε αυτήν τη Δ. Συζήτηση: Δεν υπάρχουν εγγεγραμμένα μέλη και 1 επισκέπτης