ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

#1

Επισυνάπτουμε τα σημερινά θέματα.

Καλά αποτελέσματα σε όλα τα παιδιά!

mitsos7 · #2

Καλησπέρες.. Α λυκείου εδώ. Πολύ δύσκολα τα θέματα, το 2 και το 3 (ειδικά) δεν τα άγγιξα καθόλου. Το 1ο θέμα το έλυσα ολόσωστα πλην 1 αριθμητικού, πιθανόν έχω πιάσει τουλάχιστον το μισό. Πάντως τουλάχιστον 3 εκ των 4 θεμάτων απευθύνονταν σε Β λυκείου και πάνω

Καλά αποτελέσματα σε όλους!

juan · #3

Καλησπέρα και από εμένα! Έγραψα σήμερα, στους μεγάλους, έλυσα το 1ο και το 3ο θέμα, έχοντας χτίσει ελαφρώς το 4ο. Είμαι πολύ ευχαριστημένος και καλά αποτελέσματα σε όλους!

Mathmagic24 · #4

mitsos7 έγραψε: ↑
Σάβ Φεβ 22, 2025 3:54 pm
Καλησπέρες.. Α λυκείου εδώ. Πολύ δύσκολα τα θέματα, το 2 και το 3 (ειδικά) δεν τα άγγιξα καθόλου. Το 1ο θέμα το έλυσα ολόσωστα πλην 1 αριθμητικού, πιθανόν έχω πιάσει τουλάχιστον το μισό. Πάντως τουλάχιστον 3 εκ των 4 θεμάτων απευθύνονταν σε Β λυκείου και πάνω

Καλά αποτελέσματα σε όλους!

Καλησπέρα, στο πρώτο βρήκες n=1 και m=5 ;

juan · #5

Ναι σωστά!

Mathmagic24 · #6

juan έγραψε: ↑
Σάβ Φεβ 22, 2025 4:31 pm
Ναι σωστά!

Λες να πειράζει η υπόθεση ότι οι δύο λύσεις είναι ρητές;
Ώστε να το θεωρήσουμε πολυώνυμο, να βρούμε τα m και n και με Χόρνερ τις άλλες λύσεις
Το αποτέλεσμα πάλι σωστό θα βγει (δύο πραγματικές λύσεις -1 και -4 και δύο μιγαδικές i και -i)

juan · #7

Η αλήθεια ειναι πως δεν έδινε περιορισμό για τις υπολοιπες ρίζες. Προσωπικά δεν βρήκα τις μιγαδικες αν και θεωρητικά αυστηρά μιλώντας τις ζητουσε.

Mathmagic24 · #8

juan έγραψε: ↑
Σάβ Φεβ 22, 2025 4:47 pm
Η αλήθεια ειναι πως δεν έδινε περιορισμό για τις υπολοιπες ρίζες. Προσωπικά δεν βρήκα τις μιγαδικες αν και θεωρητικά αυστηρά μιλώντας τις ζητουσε.

Τις έβαλα σε παρένθεση καλού κακού
Εφόσον στη παραγοντοποίηση βάλεις το x²+1 δε νομίζω να υπάρχει πρόβλημα

Aba · #9

Μεγάλων 1
Tο αρχικό πολυώνυμο είναι γινόμενο δύο άλλων δεύτερου βαθμού:
$P(x)=x^{4}+5x^{3}+mx^{2}+5nx+4 \Rightarrow P(x)=(x^{2}+5x+k)(x^2+ax+b)$
Θέλουμε η ισότητανα ισχύει για κάθε x επομένως καταλήγουμε στις σχέσεις : $a=0, b+k=m,b=n,bk=4 \Rightarrow n(m-n)=4\Rightarrow (n,m)=(1,5),(2,4),(4,5)$
Για αυτές τις τιμές οι ρίζες της εξίσωσης είναι αντοίστοιχα : $(-1,-4,i,-i), (\frac{-5+\sqrt{17}}{2},\frac{-5-\sqrt{17}}{2},\sqrt{2}i,-\sqrt{2}i),(\frac{-5+\sqrt{21}}{2},\frac{-5-\sqrt{21}}{2},2i,-2i)$

Panagiotis2007 · #10

juan έγραψε: ↑
Σάβ Φεβ 22, 2025 4:47 pm
Η αλήθεια ειναι πως δεν έδινε περιορισμό για τις υπολοιπες ρίζες. Προσωπικά δεν βρήκα τις μιγαδικες αν και θεωρητικά αυστηρά μιλώντας τις ζητουσε.

Εγώ βρήκα 3 ζεύγοι m,n και τρία ζεύγη x1,x2,x3,x4

Aba · #11

Πρόβλημα 3 Μεγάλων:
Για χ=y=0 : $f(0)+f(0)=10f(0) \Rightarrow f(0)=0$
Για y=0 : $f(x)+f(2x)=5f(x) \Rightarrow f(x)=\frac{1}{4}f(2x)$
Για χ=0 : $f(2y)+f(-y)=5f(y)\Rightarrow f(-y)=f(y)$
Με ισχυρή επαγωγή αποδεικνύω ότι : $f(x)=\frac{1}{n^{2}}f(nx)$ για κάθε φυσικό αριθμό.
Base case: Για n=1 προφανώς ισχύει f(x)=f(x)

και για n=2 το αποδείξαμε παραπάνω
Έστω ότι ισχύει για κάθε φυσικό μέχρι το n-1.
Για το n :
Θέτω y=2x-nx : f(x(5-2n))+f(nx)=5f(x)+5f(x(2-n))

Επειδή η f είναι άρτια : f(x(5-2n))+f(nx)=5f(x)+5f(x(n-2))

Για n>1 οι φυσικοί n-2 και 5-2n είναι μικρότεροι του n :
$f(nx)=f(x)(5+ 5(n-2)^{2}-(2n-5)^{2})\Rightarrow f(nx)=n^{2}f(x)=> f(x)=\frac{1}{n^{2}}f(nx)$
Για χ=1 : f $(1)=\frac{1}{n^{2}}f(n)\Rightarrow f(n)=n^2f(1)$ που ισχύει για όλους τους φυσικούς
Εφόσον η σχέση ισχύει για κάθε χ ρητό και n φυσικό, θεωρώ τυχόν p φυσικό : x=p/n
$\Rightarrow f(p/n)=\frac{1}{n^{2}}f(p)=\frac{p^{2}}{n^{2}}f(1)\Rightarrow f(x)=f(1)x^{2}$ με χ ρητό

sachstyl · #12

Aba έγραψε: ↑
Σάβ Φεβ 22, 2025 5:23 pm
Πρόβλημα 3 Μεγάλων:
Για χ=y=0 : $f(0)+f(0)=10f(0) \Rightarrow f(0)=0$
Για y=0 : $f(x)+f(2x)=5f(x) \Rightarrow f(x)=\frac{1}{4}f(2x)$
Για χ=0 : $f(2y)+f(-y)=5f(y)\Rightarrow f(-y)=f(y)$
Με ισχυρή επαγωγή αποδεικνύω ότι : $f(x)=\frac{1}{n^{2}}f(nx)$ για κάθε φυσικό αριθμό.
Base case: Για n=1 προφανώς ισχύει και για n=2 το αποδείξαμε παραπάνω
Έστω ότι ισχύει για κάθε φυσικό μέχρι το n-1.
Για το n :
Θέτω y=2x-nx :
Επειδή η f είναι άρτια :
Για n>1 οι φυσικοί n-2 και 5-2n είναι μικρότεροι του n :
$f(nx)=f(x)(5+ 5(n-2)^{2}-(2n-5)^{2})\Rightarrow f(nx)=n^{2}f(x)=> f(x)=\frac{1}{n^{2}}f(nx)$
Για χ=1 : f $(1)=\frac{1}{n^{2}}f(n)\Rightarrow f(n)=n^2f(1)$ που ισχύει για όλους τους φυσικούς
Εφόσον η σχέση ισχύει για κάθε χ ρητό και n φυσικό, θεωρώ τυχόν p φυσικό : x=p/n
$\Rightarrow f(p/n)=\frac{1}{n^{2}}f(p)=\frac{p^{2}}{n^{2}}f(1)\Rightarrow f(x)=f(1)x^{2}$ με χ ρητό

Αυτή ήταν η ιδέα, να τη λύσεις όπως λύνεται ουσιαστικά η συναρτησιακή του Cauchy. Όμως, η λύση σου, όπως την έχεις παραθέσει εδώ, έχει ένα μικρό θεματάκι. Τόσο η απλή, όσο και η ισχυρή επαγωγή, δουλεύουν με θετικούς ακεράιους, ενώ το 5-2n

είναι αρνητικός για $n\geqslant 3$ . Επειδή f(2x)=4f(x)

και

άρτια, αρκεί να κάνουμε επαγωγή για να δείξουμε ότι f((2k+1)x)=(2k+1)^2f(x)

για $k\geqslant 2$ (απλό για k=1

). Θέτοντας y=kx

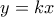και χρησιμοποιώντας την αρτιότητα της

σε συνδυασμό με την f(2x)=4f(x)

- ούτως ώστε να γράψεις $f(x(2-k))=f((k-2)x)=2^{2\ell}f(mx)$ με $k-2=2^{\ell}m, (m,2)=1$ - μπορείς να χρησιμοποιήσεις ισχυρή επαγωγή για να βγάλεις ότι f((2k+1)x)=(2k+1)^2f(x)

. Μετά συνεχίζεις όπως στη λύση σου.

Mathmagic24 · #13

Aba έγραψε: ↑
Σάβ Φεβ 22, 2025 5:23 pm
Πρόβλημα 3 Μεγάλων:
Για χ=y=0 : $f(0)+f(0)=10f(0) \Rightarrow f(0)=0$
Για y=0 : $f(x)+f(2x)=5f(x) \Rightarrow f(x)=\frac{1}{4}f(2x)$
Για χ=0 : $f(2y)+f(-y)=5f(y)\Rightarrow f(-y)=f(y)$
Με ισχυρή επαγωγή αποδεικνύω ότι : $f(x)=\frac{1}{n^{2}}f(nx)$ για κάθε φυσικό αριθμό.
Base case: Για n=1 προφανώς ισχύει και για n=2 το αποδείξαμε παραπάνω
Έστω ότι ισχύει για κάθε φυσικό μέχρι το n-1.
Για το n :
Θέτω y=2x-nx :
Επειδή η f είναι άρτια :
Για n>1 οι φυσικοί n-2 και 5-2n είναι μικρότεροι του n :
$f(nx)=f(x)(5+ 5(n-2)^{2}-(2n-5)^{2})\Rightarrow f(nx)=n^{2}f(x)=> f(x)=\frac{1}{n^{2}}f(nx)$
Για χ=1 : f $(1)=\frac{1}{n^{2}}f(n)\Rightarrow f(n)=n^2f(1)$ που ισχύει για όλους τους φυσικούς
Εφόσον η σχέση ισχύει για κάθε χ ρητό και n φυσικό, θεωρώ τυχόν p φυσικό : x=p/n
$\Rightarrow f(p/n)=\frac{1}{n^{2}}f(p)=\frac{p^{2}}{n^{2}}f(1)\Rightarrow f(x)=f(1)x^{2}$ με χ ρητό

Αν έγραψα αυτό και το άφησα στο f(n)=n^2f(1)

και έθεσα n ρητό πόσο λες να μου κόψουν;

panoslovesimop4 · #14

Καλησπέρα. Θα μπορούσε κάποιος να παραθέσει λύση στη γεωμετρία?

Aba · #15

sachstyl έγραψε: ↑
Σάβ Φεβ 22, 2025 5:45 pm

Aba έγραψε: ↑
Σάβ Φεβ 22, 2025 5:23 pm
Πρόβλημα 3 Μεγάλων:
Για χ=y=0 : $f(0)+f(0)=10f(0) \Rightarrow f(0)=0$
Για y=0 : $f(x)+f(2x)=5f(x) \Rightarrow f(x)=\frac{1}{4}f(2x)$
Για χ=0 : $f(2y)+f(-y)=5f(y)\Rightarrow f(-y)=f(y)$
Με ισχυρή επαγωγή αποδεικνύω ότι : $f(x)=\frac{1}{n^{2}}f(nx)$ για κάθε φυσικό αριθμό.
Base case: Για n=1 προφανώς ισχύει και για n=2 το αποδείξαμε παραπάνω
Έστω ότι ισχύει για κάθε φυσικό μέχρι το n-1.
Για το n :
Θέτω y=2x-nx :
Επειδή η f είναι άρτια :
Για n>1 οι φυσικοί n-2 και 5-2n είναι μικρότεροι του n :
$f(nx)=f(x)(5+ 5(n-2)^{2}-(2n-5)^{2})\Rightarrow f(nx)=n^{2}f(x)=> f(x)=\frac{1}{n^{2}}f(nx)$
Για χ=1 : f $(1)=\frac{1}{n^{2}}f(n)\Rightarrow f(n)=n^2f(1)$ που ισχύει για όλους τους φυσικούς
Εφόσον η σχέση ισχύει για κάθε χ ρητό και n φυσικό, θεωρώ τυχόν p φυσικό : x=p/n
$\Rightarrow f(p/n)=\frac{1}{n^{2}}f(p)=\frac{p^{2}}{n^{2}}f(1)\Rightarrow f(x)=f(1)x^{2}$ με χ ρητό
Αυτή ήταν η ιδέα, να τη λύσεις όπως λύνεται ουσιαστικά η συναρτησιακή του Cauchy. Όμως, η λύση σου, όπως την έχεις παραθέσει εδώ, έχει ένα μικρό θεματάκι. Τόσο η απλή, όσο και η ισχυρή επαγωγή, δουλεύουν με θετικούς ακεράιους, ενώ το είναι αρνητικός για $n\geqslant 3$ . Επειδή και άρτια, αρκεί να κάνουμε επαγωγή για να δείξουμε ότι για $k\geqslant 2$ (απλό για ). Θέτοντας και χρησιμοποιώντας την αρτιότητα της σε συνδυασμό με την - ούτως ώστε να γράψεις $f(x(2-k))=f((k-2)x)=2^{2\ell}f(mx)$ με $k-2=2^{\ell}m, (m,2)=1$ - μπορείς να χρησιμοποιήσεις ισχυρή επαγωγή για να βγάλεις ότι . Μετά συνεχίζεις όπως στη λύση σου.

Ναι, δεν το είχα δει αυτό. Ευχαριστώ για την διόρθωση!

Belias · #16

Για το θεμα 4 των senior
Θελουμε y^2+108=a^3

Παίρνωντας $mod \: 9$ βλέπουμε $y^2 \equiv a^3$ δηλαδη $y^2 \equiv 1 (mod \: 9)$
H έκφραση y^2=a^3-108

αποτελεί ελλειπτική καμπύλη
Για y=0

έχω

Άτοπο
Για να έχει λύσεις πρέπει το y|108

άρα το

Όμως το

δεν είναι πολ.9 άρα πρέπει y|4

και ελέγχωντας τις περιπτώσεις βλέπουμε ότι $y \in \emptyset$
Σωστό είναι?

juan · #17

sachstyl έγραψε: ↑
Σάβ Φεβ 22, 2025 5:45 pm

Aba έγραψε: ↑
Σάβ Φεβ 22, 2025 5:23 pm
Πρόβλημα 3 Μεγάλων:
Για χ=y=0 : $f(0)+f(0)=10f(0) \Rightarrow f(0)=0$
Για y=0 : $f(x)+f(2x)=5f(x) \Rightarrow f(x)=\frac{1}{4}f(2x)$
Για χ=0 : $f(2y)+f(-y)=5f(y)\Rightarrow f(-y)=f(y)$
Με ισχυρή επαγωγή αποδεικνύω ότι : $f(x)=\frac{1}{n^{2}}f(nx)$ για κάθε φυσικό αριθμό.
Base case: Για n=1 προφανώς ισχύει και για n=2 το αποδείξαμε παραπάνω
Έστω ότι ισχύει για κάθε φυσικό μέχρι το n-1.
Για το n :
Θέτω y=2x-nx :
Επειδή η f είναι άρτια :
Για n>1 οι φυσικοί n-2 και 5-2n είναι μικρότεροι του n :
$f(nx)=f(x)(5+ 5(n-2)^{2}-(2n-5)^{2})\Rightarrow f(nx)=n^{2}f(x)=> f(x)=\frac{1}{n^{2}}f(nx)$
Για χ=1 : f $(1)=\frac{1}{n^{2}}f(n)\Rightarrow f(n)=n^2f(1)$ που ισχύει για όλους τους φυσικούς
Εφόσον η σχέση ισχύει για κάθε χ ρητό και n φυσικό, θεωρώ τυχόν p φυσικό : x=p/n
$\Rightarrow f(p/n)=\frac{1}{n^{2}}f(p)=\frac{p^{2}}{n^{2}}f(1)\Rightarrow f(x)=f(1)x^{2}$ με χ ρητό
Αυτή ήταν η ιδέα, να τη λύσεις όπως λύνεται ουσιαστικά η συναρτησιακή του Cauchy. Όμως, η λύση σου, όπως την έχεις παραθέσει εδώ, έχει ένα μικρό θεματάκι. Τόσο η απλή, όσο και η ισχυρή επαγωγή, δουλεύουν με θετικούς ακεράιους, ενώ το είναι αρνητικός για $n\geqslant 3$ . Επειδή και άρτια, αρκεί να κάνουμε επαγωγή για να δείξουμε ότι για $k\geqslant 2$ (απλό για ). Θέτοντας και χρησιμοποιώντας την αρτιότητα της σε συνδυασμό με την - ούτως ώστε να γράψεις $f(x(2-k))=f((k-2)x)=2^{2\ell}f(mx)$ με $k-2=2^{\ell}m, (m,2)=1$ - μπορείς να χρησιμοποιήσεις ισχυρή επαγωγή για να βγάλεις ότι . Μετά συνεχίζεις όπως στη λύση σου.

Αυτο έκανα!! χαχαχα νιώθω πολύ χαρούμενος τώρα.

Mathmagic24 · #18

Belias έγραψε: ↑
Σάβ Φεβ 22, 2025 6:04 pm
Για το θεμα 4 των senior
Θελουμε
Παίρνωντας $mod \: 9$ βλέπουμε $y^2 \equiv a^3$ δηλαδη $y^2 \equiv 1 (mod \: 9)$
H έκφραση αποτελεί ελλειπτική καμπύλη
Για έχω Άτοπο
Για να έχει λύσεις πρέπει το άρα το
Όμως το δεν είναι πολ.9 άρα πρέπει και ελέγχωντας τις περιπτώσεις βλέπουμε ότι $y \in \emptyset$
Σωστό είναι?

Σωστό αν και λογικά υπάρχει τρόπος χωρίς έλλειψη με συνδυασμό mod 7 και mod 9

Belias · #19

Εγώ είμαι α λυκείου χωρίς σοβαρές διακρίσεις στο παρελθόν (χωρίς μετάλλιο στους 2 προηγούμενους Αρχιμήδηδες). Φέτος είχα προετοιμαστεί κάπως καλύτερα. Μου φάνηκαν δύσκολα τα θέματα γενικά. Στο 1ο απέδειξα (εσφαλμένα) $m+n \geq 125$ ονομάζοντας τις 2 πραγματικές ρίζες του πολυωνύμου και αφαιρώντας κατά μέλη. Στο 2ο κοίταγα λάθος τρίγωνα και έψαχνα Ceva μέχρι που 5 λεπτά πριν το τέλος συνειδητοποίησα την καθετότητα των 2 σεβιανών άρα αρκούσε η ΑΡ να είναι κάθετη στη ΜΝ. Αυτό ισοδυναμούσε με ένα τετράπλευρο να είναι εγγράψιμο αλλά προφανώς δε πρόλαβα να το αποδείξω. Στο 3ο απέδειξα ότι η f είναι άρτια χωρίς να καταλήξω κάπου στην κατασκευή μου (προσπάθησα επαγωγικά αλλά δεν βγήκε). Και στο 4 δοκίμασα να το αποδείξω με ισχυρή επαγωγή αλλά δεν το κατάφερα. Οπότε μάλλον χωρίς μετάλλιο και φέτος, εκτός άμα ο Παντοδύναμος κάνει κάνα θαύμα... Ξέρουμε γιατί δεν υπήρχε συνδυαστική σε κανένα από τα 8 θέματα σήμερα?

#20

Belias έγραψε: ↑
Σάβ Φεβ 22, 2025 6:04 pm
H έκφραση αποτελεί ελλειπτική καμπύλη

Πώς χρησιμοποιείς ότι είναι ελλειπτική καμπύλη; Χρησιμοποιείς κάποιο Θεώρημα; Γιατί πρέπει $y\mid 108$ ;

ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Re: ΑΡΧΙΜΗΔΗΣ 2024-2025 (ΘΕΜΑΤΑ-ΛΥΣΕΙΣ)

Μέλη σε σύνδεση